1. 벡터
- Vector = Magnitude(크기) + Dirrection(방향)
크기는 벡터의 길이이고 방향은 벡터가 가리키는 방향이다. - Scalar : 크기만 갖는 양
- R의 n승 = n dimensional real-coordinate space (n차원 실수좌표공간)
- Vector 에 Scalar 을 곱하는 것은 방향을 바꾸지 않는다. 크기만 늘어난다.
- x와 y 라는 벡터의 뺄셈은 두 벡터의 차이를 구하게 된다.
- Unit Vector[단위벡터] : 열벡터랑 다르게 크기가 1인 벡터이다.

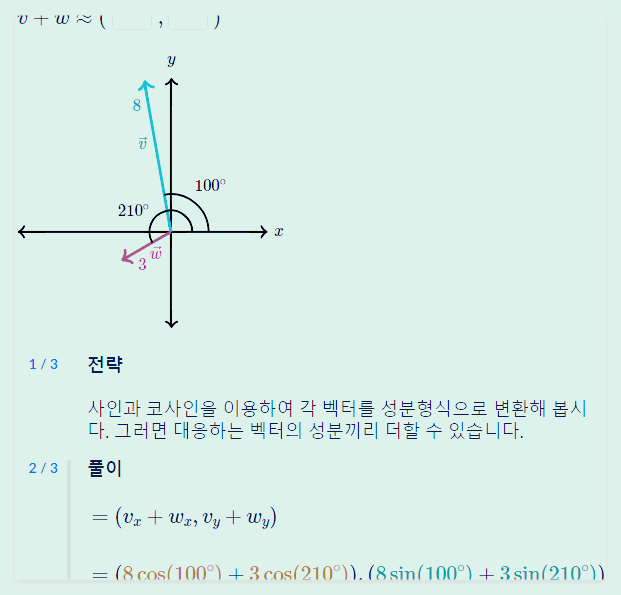
- 삼각함수를 계산할 때 각도는 반드시 양의 x축부터 그어서 돌리면 된다.
- cos 값은 270~90 [0~90, 270~360] 은 양수값, 90~270은 음수값이다.
- sin 값은 0~180 은 양수값, 180~360 은 음수값이다.
- 직선의 매개변수 표현 L = { P1 + t(P1 - P2) | t ∈ R }
3차원부터는 직선방정식을 표현하기가 어려워진다. 유일한 방법이 매개변수 방정식이다. n차원의 직선이 되는 벡터의 집합을 정의할 수 있다.
2. 선형결합과 생성
Linear Combination
Span (A, B) = R^2
벡터 2개를 잡았을 때 각각에 상수배를 해주면 R^2 즉 모든 곳에 놓일 수 있게 된다.
모두가 그런 것은 아니다. A = [2 2] B = [-2 -2] 라면 한 직선에서만 움직일 수 있다.
벡터 v1, v2, ... , vn 으로 이루어진 집합의 생성 : 집합의 생성은 벡터들을 모은다.
Span (v1, v2, ... , vn) = {c1v1 + c2v2 + ... + cnvn }
어떤 수를 잡아도 벡터들의 선형 결합으로 나타낼 수 있다.
3. 선형종속과 독립
선형종속 : linearly dependent set
집합의 한 벡터를 집합의 다른 벡터의 선형결합으로 나타낼 수 있는 것이다.
v1 = [2 3]과 v2 = [4 6]은 크기는 다르지만 방향은 같은 것이다. v2 = 2*v1
선형독립 : linearly independent set
벡터에 어떤 값을 곱하더라도 서로에 대한 선형결합으로 나타낼 방법이 없다.
v1 = [2 3] , v2 = [7 2] , v3 = [9 5]
상관없어보이지만 v1 + v2 = v3 이다.
v1과 v2를 더했을 때 이미 R^2 를 나타낼 수 있기 때문에 v3는 여분의 벡터이다. R^2를 생성하는 데 도움이 되지 않는다.
선형종속인지 선형독립인지 알 수 있는 유용한 방법
c1v1 + c2v2 + ... + cnvn = 0 [ 0 ... 0 ]
모두가 0일 필요는 없다. 적어도 하나만 0이 아닌 것이 있으면 참이다.
c1, c2, cn 중에 적어도 하나가 0이 아니면 선형종속임을 말한다.
모든 상수배가 0인 것밖에 방법이 없다면 그것은 선형독립임을 말한다.
4. 부분공간과 부분공간의 기저
V 가 R^n의 부분공간(subspace) 라면 3가지를 의미한다.
1. V contains 0 [0 ... 0] (영벡터)
2. 벡터 X in V → c*X in V : 스칼라 곱셈에 대해 닫혀있다.
3. 벡터 A in V, B in V → A+B in V : 벡터 덧셈에 대해 닫혀있다.
예: V = span ( [ 1 1 ] )
기울기가 1인 직선이다. (0,0)을 포함하고, 어떤 수를 곱해도 직선에 놓이고, 다른 값끼리 더해도 직선에 놓인다.
기저(basis)는 공간을 생성하는데 필요한 최소한의 벡터집합이다.
부분공간이 존재한다고 하나의 기저만 존재하는 것은 아니다. 무한 개가 존재한다.
T = { [1 0], [0 1] } 이것이 표준 기저 집합이다. standard basis set. 즉 단위 벡터 i 와 j 가 되는 것이다.
부분공간에서의 어떠한 벡터도 표현할 수 있다
부분공간의 기저가 있다면 기저 벡터들의 유일한 결합으로 표현될 것이다.
5. 벡터의 내적과 외적
내적 : dot product
벡터의 길이 : 제곱해서 루트 씌우는 것이다.
벡터 자신을 내적하면(곱하면) 어떻게 될까?
길이의 제곱은 벡터 a와 그 자신을 내적한 것과 같다.
벡터 내적의 성질 증명
교환법칙이 성립한다. V · W = W · V
분배법칙이 성립한다. (V+W) · X = (V · X) + (W · X)
(cV) · W = c(V · W)
코시-슈바르츠 부등식의 증명
두 벡터의 내적의 절댓값은 두 벡터의 길이의 곱보다 작거나 같다.
두 벡터의 내적이 두 벡터의 길이의 곱과 같아지는 경우는! 하나의 벡터가 다른 벡터의 스칼라배인 경우뿐이다.
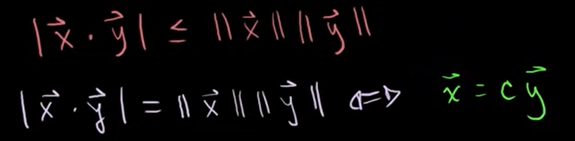
벡터의 삼각부등식

2차원의 데카르트 좌표를 넘어서 100차원에서도 적용할 수 있는 것이다.
벡터 사이의 각 정의하기
벡터의 삼각부등식에 따르면 각 변의 길이는 나머지 두 변의 길이의 합보다 작거나 같다.
코사인 법칙 : c2 = a2 + b2 − 2ab*cosA
이 법칙을 a, b, a-b 를 변으로 하는 삼각형에 대입하면 다음 공식을 이끌어낼 수 있다. 매우 중요하다.
a · b = ||a||*||b||*cosA
각도가 90˚이면, cos90이 0이므로 a · b = 0 이다.
단, a와 b중 영벡터가 있으면 그것은 성립이 안 된다.
영벡터가 아니면서 a · b = 0 이라면, 그것은 수직이라 말할 수 있다.동시에 직교하는 것이다.
영벡터는 모든 벡터와 직교한다. 직교한다면 영벡터여도 괜찮다. 수직은 아니다. (수직: perpendicular, 직교: orthogonal)
점과 법선벡터를 이용하여 R3에서 평면 정의하기
법선벡터 : 면의 모든 벡터에 직각을 이루는 벡터. (normal vector)
3차원에 면이 있다면 원점으로부터 그 면에 도달하는 벡터 X1 과 X2 가 있다고 했을 때,
이 사이를 지나가는 벡터는 면 위에 위치한다. X1 - X2 이다. 이 벡터는 법선벡터 n과 직각을 이룬다.
n · (X1 - X2 ) = 0
이것을 x, y, z 축의 벡터로 내적했을 때 식이 나오는데, ax + by + cz = d 라는 형태가 나온다.
3차원 공간에서 면에 대한 보편적인 식이다.
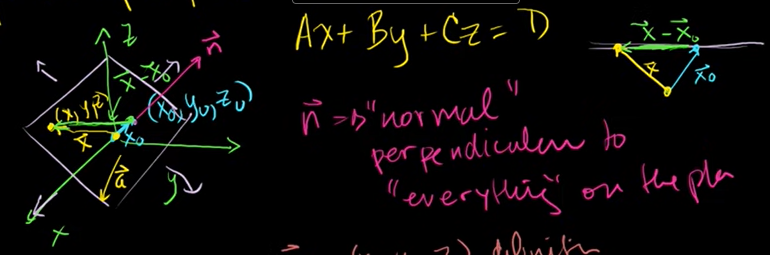
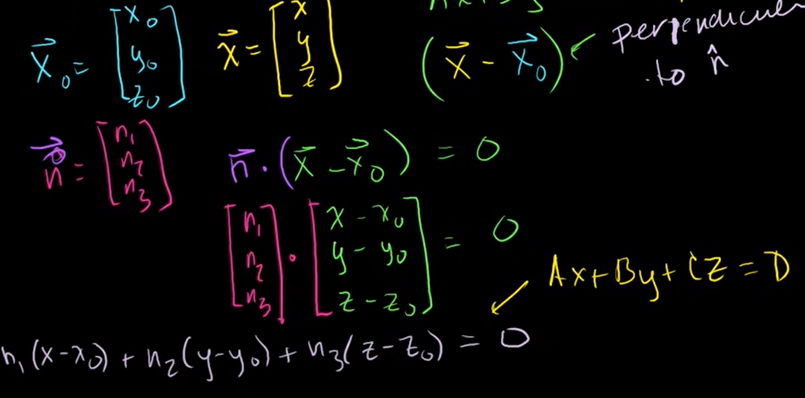
벡터의 외적
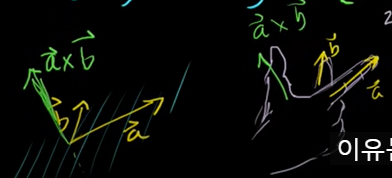
cross product
내적이 모든 차원에서만 가능했다. 외적(cross product)은 3차원에서만 가능하다.
내적의 결과가 scalar 로 나왔다면, 외적의 결과는 vector 로 나온다.
결과값인 vector 가 외적을 취하는 두 벡터에 직교한다.


증명: 외적과 각의 사인값 사이의 관계
내적.. 벡터 사이의 각 : a · b = ||a|| * ||b|| * cosA
외적.. 벡터 사이의 각 : ||a x b|| = ||a|| * ||b|| * sinA
내적은 cos 이고 외적은 sin 이다.
내적과 외적의 비교 / 직관
내적
a · b = ||b|| * ||a|| * cosA
||a||cosA = 이웃한 변
벡터 b 의 길이에 벡터 b와 같은 방향으로 나아가는 벡터 a의 크기만큼을 곱해준다는 뜻이다.
벡터 a는 벡터 b와 겹치게 된다. 그렇지만 더 큰 내적 값을 갖게 된다.
내적(dot product)은 얼마나 두 벡터가 같은 방향을 향하고 있는지를 말해준다.
같은 방향을 향하는 벡터 길이의 곱과 같다.
만약 a · b = 0 이라면 수직이다. a라는 벡터의 어느 일부로 벡터 b와 같은 방향이 없다. 0에 벡터 b를 곱하는 것이다.
최대는 cos0 =1 일 때 같은 방향의 직선이 되면서 나온다.
외적
||a x b|| = ||b|| * ||a|| * sinA
||a||sinA = 대변
벡터 b의 길이에 벡터b의 수직한 방향에 벡터 a의 일부를 곱한다.
만약 a와 b가 수직이라면 sin90=1 이므로, ||a x b|| = ||a|| * ||b|| 이다. 최대가 나온다.
만약 a와 b가 수평이라면 sin0 = 0 이므로 최소값이 된다.
수직일 때는 외적이 최대가 되고, 수평일 때는 내적이 최대가 된다.
또 신기한 것 한가지!
두 벡터의 외적의 절대값은 두 벡터로 만들어지는 평행사변형의 넓이와 같다.

벡터 삼중곱 전개 (라그랑즈 공식)
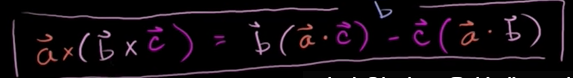
꼭 알 필요는 없지만 정말 복잡한 벡터가 있거나 수학대회라면 내적으로 풀었을 때 더 빨리 할 수 있다.
평면방정식의 법선벡터
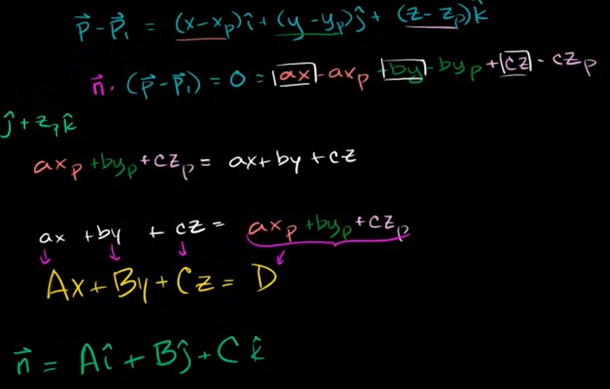
3차원 공간에 어떤 면이 있다면 그 방정식은 Ax + By + Cz = D 이다.
법선벡터의 공식은 n = ai + bj + ck
이 때, n · (P-P1) = 0 공식을 풀이해보면 a=A, b=B, c=C 이다.
따라서, 법선벡터인 n = Ai + Bj + Ck 라고 간편하게 알 수 있는 것이다.
D는 면을 이동시키기는 해도 면이 기울어진 정도에는 영향을 주지 않는다.
점과 평면 사이의 거리
최단거리를 구하려면 cos 를 이용해야 하는데 각도를 모른다. 각도를 알기 위해 그 벡터와 법선벡터 사이의 각도를 구하자.
최단거리는 벡터와 법선벡터의 내적값을 법선벡터의 크기로 나눈 것과 같다.

평면 사이의 거리
한 평면에 존재하는 세 개의 점을 찍고 두 개의 벡터를 얻는다.
그 벡터를 서로 외적하면 법선벡터를 구한다.
평면 위에 있는 임의의 점과 평면 위에 찍은 선을 잇는 벡터를 구하고 이것을 법선벡터와 내적하면 0이다.
이를 풀어보면 평면의 방정식을 구할 수 있다.
이 평면이 방정식이 주어진 평면과 평행하기 때문에 기울기가 같다.
위에서 알아본 점과 평면 사이의 거리를 구하는 공식을 적용하면 결국 방정식을 풀 수 있다.

6. 가감법으로 연립방정식을 풀기 위한 행렬
행 사다리꼴 행렬을 이용하여 3차연립방정식과 4개의 변수 풀기
어떠한 방정식이든 행렬로 대체할 수 있다. 첨가행렬 : augmented matrix
행에 첫 번째로 계수로 1이 있다면 다른 모든 계수들이 0이 되도록 만드는 것이 '기약행사다리꼴'이다. (reduced row-echelon form)
각 열에서 유일하게 0이 아닌 수를 구한다. 이것을 피벗성분(pivot entry)이라고 한다.
이것을 방정식 형태로 바꾸면 상수가 붙지 않은 피벗변수라고 한다. (pivot variable)
상수가 붙은 변수는 자유변수이다. (free variable)

행렬을 이용하여 연립일차방정식 풀기

첨가행렬로 만들고 하나의 계수만 1로 남긴채 같은 열의 다른 계수들은 0으로 만든다.
이렇게 기약행사다리꼴을 만들게 되면 각각의 변수값이 무엇인지 알게 된다.
행 사다리꼴을 이용하여 선형계는 해가 없다는 것을 알아보기
네 개의 변수가 있는 세 개의 식.
무한한 해가 있다고 생각했을 수 있지만 0 = 3처럼 해가 없으면 4차원의 공간에서 교차하지 않는 것이다. 평행하다.
총 3가지의 경우의 수가 있다.
1. 0 = a ⇒ no solution
2. unique solution
3. no unique. 무한한 해가 있다.
7. 영공간과 열공간
행렬 벡터의 곱
벡터의 길이가 매트릭스의 열의 개수와 같을 때, 곱셈을 정의할 수 있다.
벡터는 소문자, 매트릭스는 대문자이다.
벡터들을 행벡터 또는 열벡터로 전환하기 위해서는 전치시키면 된다.
매트릭스 X 벡터 =
1. 행벡터의 내적 : 매트릭스의 행을 곱하려는 벡터와 내적시킨 것과 같다.
2. 열벡터의 선형조합 : 행렬의 열벡터들의 선형조합을 만들어내는 것과 같다.
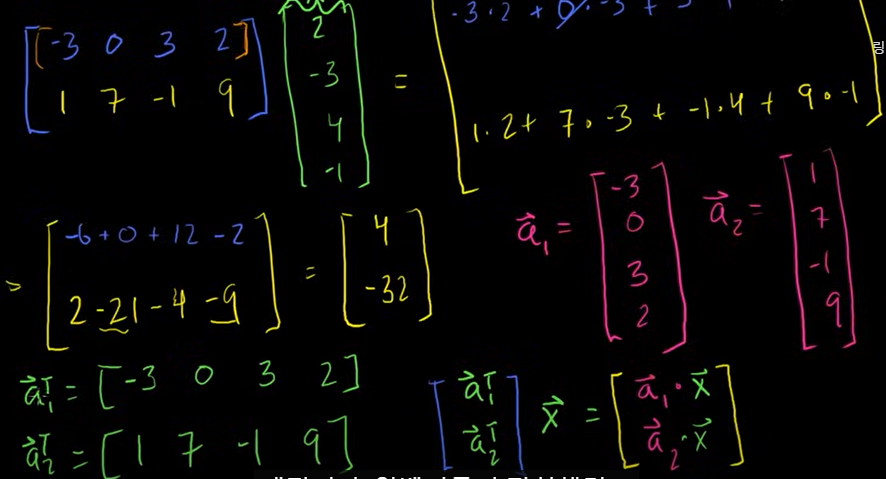
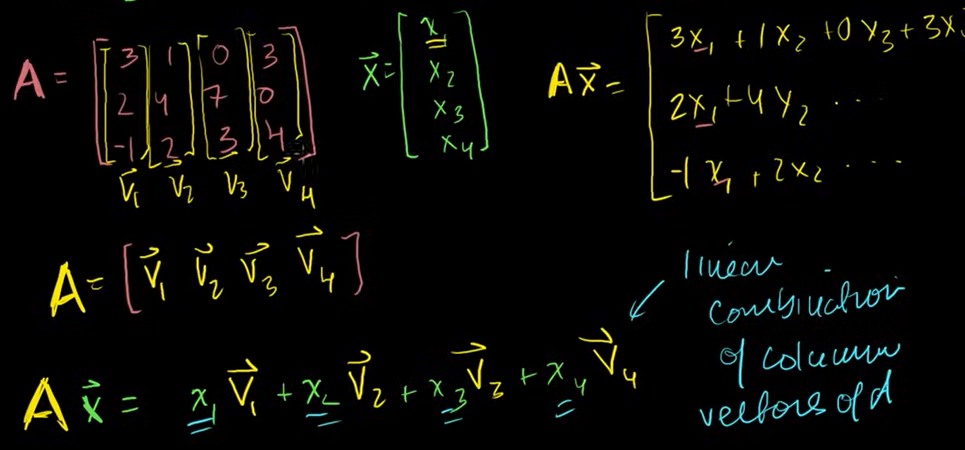
행렬의 영공간
부분공간이 되려면 갖춰야 하는 조건 3가지
1. 영벡터가 포함되어야 한다. 2. 벡터들의 합이 부분집합에 포함되어야 한다. 3. 스칼라배한 벡터가 포함되어야 한다.
행렬과 벡터의 곱이 영벡터가 나오는 것을 증명.
행렬 A와 영벡터의 곱은 영벡터가 된다. 영벡터는 N이라는 부분집합의 원소이다.
A*V1 + A*V2 = 영벡터
A*(c*V1) = c * (A*V1) = 영벡터
따라서, N은 A의 영공간이다. (nullspace)
영공간은 행렬과 곱했을 때 영벡터가 나오는 모든 벡터의 집합이다.
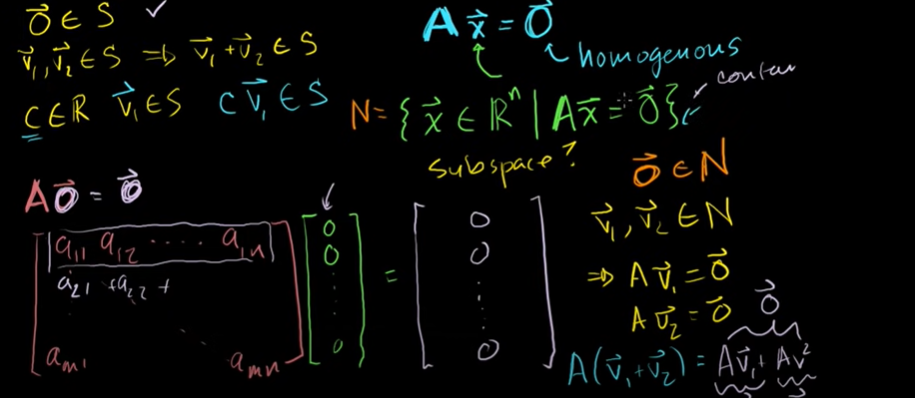
행렬의 영공간 계산하기
영공간을 구하다 보면 왼쪽 벡터와 오른쪽 벡터의 일차결합으로 구해진다.
두 벡터의 일차결합은 span 이다.
행렬 A를 긴 첨가행렬로 만들지 않고도 기약행사다리꼴로 만든 다음 영공간을 구하면 된다.
N(A) = N(rref(A))
선형 독립과의 관계
벡터에 곱해진 모든 상수배가 0이라면 선형 독립이 된다.
반대로, 선형 독립이라면 벡터에 곱해진 모든 상수배가 0이라는 뜻이다.
선형 독립이라는 것은 벡터가 다른 벡터들의 선형결합에 의해서 만들어질 수 없다는 뜻이다.
이렇게 되면 A라는 행렬의 영벡터 집합인 N(A) 는 영벡터만 존재하게 된다.
매트릭스의 영공간이 제로벡터를 포함한다면 그 매트릭스의 열이 선형독립한다는 뜻이다.

행렬의 열공간
열공간 [Column Space]
열공간은 유효한 부분공간이다. 똑같이 영벡터가 포함되고 더하기와 곱셈에 대해 닫혀 있다
벡터들의 선형결합으로 만들 수 있는 열공간.
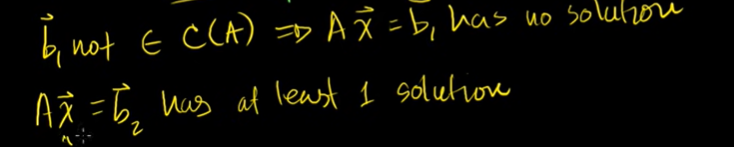
b1 이 열공간에 포함되지 않는다면 Ax = b1 은 해가 없다.
Ax = b2 가 적어도 하나의 해가 있다면 b2는 A의 열공간인 C(A)의 원소라는 뜻이다.
영공간과 열공간의 기저
열공간은 행열 A의 열벡터의 너비와 같다. 그 선형결합들을 span으로 묶으면 된다.
영공간은 각 열의 영공간과 같다. 행열 A의 기약행 사다리꼴의 영공간과도 같다.
영공간을 구했을 때 영벡터만 나온다면 선형독립이다. 더불어, 열공간도 선형독립이라 할 수 있다.
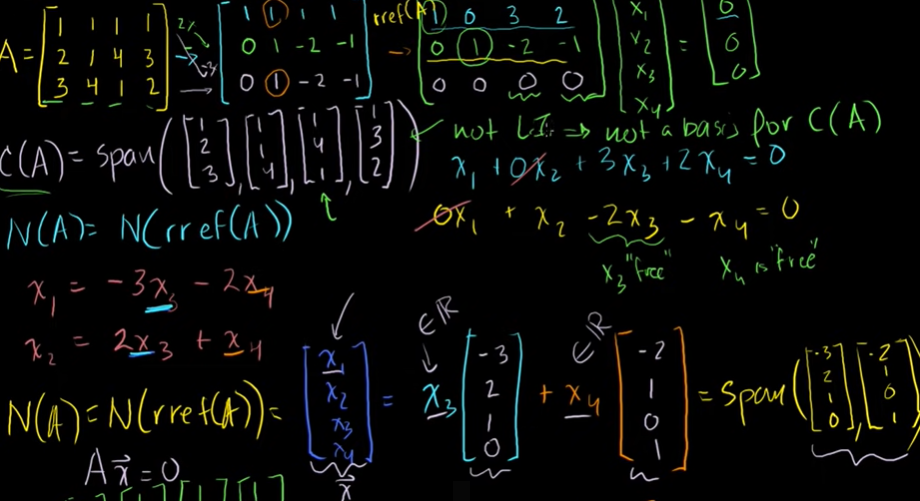
위 문제에서는 영공간의 벡터집합이 영벡터가 아니다. x3와 x4에 0 을 대입하면 0이 되기는 하지만 항상 영벡터가 되는 것은 아니다. 영공간이 선형독립이 아니기 때문에 열공간도 선형독립이 아니다.
기저는 부분공간을 생성하는 벡터집합이다. 기저 또한 선형독립성을 지닌다.
열공간의 기저를 찾기 위해서는 중복벡터를 없애야 한다.
기저는 A의 행 공간을 생성하는 벡터이다.
대입을 해봐서 두 개의 벡터로 다른 벡터가 생성이 되면 그 다른 벡터는 기저가 아닌 것이다.
예를 들어, x3를 0으로, x4를 -1로 둔다면 x4가 x1, x2로 만들어지는지 알 수 있다.
R3에 있는 열공간을 평면으로 시각화하기
R3 안에 어떤 평면을 구하게 된다.
기저가 되는 벡터 두 개를 외적하면 수직하는 법선벡터를 구하게 된다.
이 법선벡터를 임의의 점과 기저벡터를 잇는 벡터와 내적하면 0이 된다.
그러면 평면에 대한 방정식이 나온다.
정리하자면, 열 생성의 기저를 찾고 두 기저벡터의 외적 이용해 법선벡터를 찾은 후 법선벡터와 이 평면에서 기저벡터 하나를 뺀 벡터와의 내적을 이용해 구했다.
다른 방법!
기저벡터들은 자기자신들의 열공간에 존재한다.
Ax = b 라고 두고 어떤 b가 유효한 값이 나오는지 확인한다.
유효한 해가 나오려면 b는 꼭 0이 되어야 한다.
기약행사다리꼴의 한 행을 다 0으로 만든다.

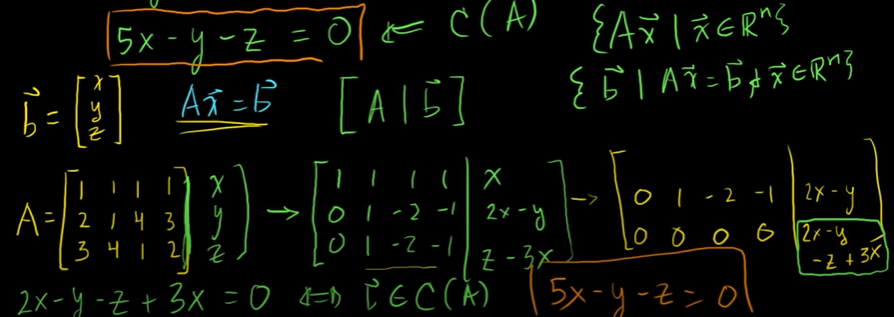
증명: 어떠한 부분공간의 기저도 원소의 수가 같습니다
집합 A보다 적은 원소를 가질 수 없다.
영공간의 차원
영공간을 구한다. 영공간의 벡터가 선형독립적이라면 기저가 된다는 것을 알 수 있다.
B의 기저 집합 안에 벡터의 개수가 B라는 영공간의 차원이다.
B라는 영공간의 차원은 B의 무효성이라고도 한다.
행열 A의 무효성은 A의 기약행사다리꼴에 존재하는 피보트가 아닌 열의 개수이다.
자유변수의 개수는 다른 벡터들의 선형결합식으로 나타낼 수 없는 벡터들의 개수이다.
변수의 개수는 영공간의 기저 안의 벡터의 개수가 된다.

열공간의 차원
A의 열벡터의 기저를 찾아보자.
기약행사다리꼴에서 피보트 성분이 있으면 확실히 선형독립한다는 것을 알 수 있다.
왜냐면 하나만 1을 가지고 있고 다른 것은 0이기 때문이다. 0에 무엇을 곱해도 0이 된다.
피보트가 아닌 열들은 피보트 열들로 표현이 가능하다. 피보트가 있는 벡터들의 선형결합으로 가능한 것이다.
열공간의 차원은 열공간의 기저 안에 있는 벡터의 개수이다.
모든 열공간을 생성하는 선형독립인 열벡터들의 개수이다.

영공간의 차원은 피봇이 아닌 열벡터의 개수이고
열공간의 차원은 피봇인 열벡터의 개수이다.
기저 열과 축열 사이의 관계
왜 그저 대응하는 열을 취할 수 있는 것일까? 왜 이 열들이 선형독립일까? 기저 벡터를 이용하여 선형결합들을 만들 수 있을까?
기약행사다리꼴의 추축열은 모두 선형독립이다. 1이 유일한 추축열이다.
Rx = 0 이 되는 c1, c2, c4 값은 모두 0이다. 따라서 선형독립이라 할 수 있다.

후보 기저의 A의 열공간 생성
a3, a5 는 a1, a2, a4로도 표현이 가능하기에 필요없게 된다.
'Mathematics and Statistics' 카테고리의 다른 글
| Review >> Essence of Linear Algebra_3Blue1Brown (1) | 2024.01.14 |
|---|---|
| Essence of Linear Algebra_3Blue1Brown (2) | 2024.01.14 |
| Review >> Linear Algebra_Khan (2) | 2024.01.09 |
| Linear Algebra_Khan [3/3] 상호 좌표계(기저) (1) | 2024.01.09 |
| Linear Algebra_Khan [2/3] 행렬변환 (2) | 2024.01.03 |
