1. 직교보공간
직교여공간
Orthogonal Complement
어떤 부분공간이 있고 모든 원소와 직교하는 벡터들이 원소로 있는 어떤 집합을 구할 때,
그 벡터의 집합은 V의 직교보공간이다. V perp (perpendicular) 이다.
부분공간을 위한 조건 : 더한 것과 스칼라배에 대해서, 영벡터가 포함되어야 한다.

영공간은 행공간의 직교여공간이다.
r 의 전치와 x의 내적은 0과 같다.
행렬의 행들에 직교한다면 선형결합과도 직교한다는 뜻이다.
행벡터의 선형결합인 임의의 벡터를 영공간의 임의의 원소와 내적하면 0이다.
영공간의 모든 원소는 행공간의 원소와 모두 직교한다.
영공간의 모든 원소는 직교여공간의 원소이다.
반대로, 직교여공간의 모든 원소가 영공간의 원소이다.
즉, A의 영공간은 A의 행공간(전치의 열공간)의 직교여공간과 같다.
좌영공간(전치의 영공간)은 열공간의 직교여공간과 같다.
dim(v) + dim(v의 직교여공간) = n
V라는 집합이 A의 열공간일 때
V의 직교여공간은 A 열공간의 직교여공간과 같기 때문에 A 전치의 영공간(좌영공간)의 계수와 같다.
자유벡터의 갯수는 영공간의 차원을 말한다.
열공간의 기저와 영공간의 기저를 더하면 전체 열의 수(n)가 된다.
A 전치의 rank + A 전치의 영공간 = A 전치행렬의 열 (n)
A 전치의 계수는 A의 계수와 같다. 전치행렬을 해도 계수가 바뀌지 않는다.


부분공간의 원소를 이용하여 Rn의 벡터를 나타내기
어떤 부분공간이며 동시에 그것의 직교여공간의 유일한 벡터는 영벡터이다.
직교여공간의 차원은 n-k 이다.
차원은 기저를 형성하기 위한 선형독립한 벡터의 개수이다.
부분공간과 그것의 직교여공간 을 합치면 R^n 전체에 대한 기저를 알 수 있을까?
선형결합의 모든 상수들이 0이 되는 것밖에 해가 없다면 벡터들은 선형독립이 되고 기저라고 할 수 있다.
v라는 부분공간을 결합하는 상수들도 모두 0이 되는 것이고, v의 직교여공간을 결합하는 상수들도 모두 0이다.
c1~ck, d1~d(n-k) 모두 0이다.
이것들과 붙어있는 모든 벡터들이 선형독립이다.
옛날에 배우기를,
n차원의 부분공간(R^n) 이 존재할 때 그에 속하는 n개의 선형독립하는 벡터가 있으며
n개의 벡터의 집합은 부분공간의 기저가 된다.
앞서 살펴본 벡터들의 갯수는 k + (n-k) = n개이다. 이들이 기저가 되는 것이다.
따라서, 부분공간이 주어지면 그 직교여공간을 구할 수 있다.
R^n의 원소를 부분공간 V의 벡터와 직교여공간의 벡터의 합으로 나타내는 것은 유일한 방법만 있다.
직교여공간의 직교여공간
V의 직교보공간에 수직이지만 V밖에 있는 공간이 존재할 수 있다.
x · w = 0 이다.
x는 v의 직교보공간의 직교보공간인데 이것은 w(v의 직교보공간)과 서로 수직이기 때문이다.
이것을 계산해보면 w = 0 이 나온다.
따라서, x = v 이다.
V의 직교여공간의 직교여공간의 원소인 x 는 기존 부분공간 V의 원소가 된다.
그러므로 직교보공간의 직교보공간에는 있지만 기존의 부분공간에는 없는 원소는 존재하지 않는다.
모든 것은 V 안에 있어야 한다.

벡터 v 는 벡터 w와 벡터 x 의 합으로 만들어질 수 있는 것이다.
V의 직교보공간과 V의 직교보공간의 직교보공간으로 만들어질 수 있다.
벡터 v 가 V의 원소라면, 벡터 v는 V의 직교여공간의 직교보공간의 원소이기도 하다.
v = (V ㅗ) ㅗ
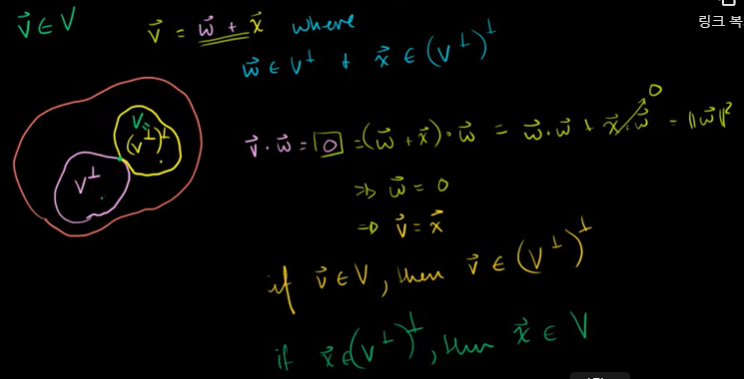
영공간의 직교여공간
A의 행공간의 직교여공간은 A의 영공간이다.
A의 열공간의 직교여공간은 A의 좌영공간이다.
A의 영공간의 직교여공간은? A의 행공간이다.(A의 전치의 열공간)
A의 좌영공간의 직교여공간은? A의 열공간이다.
Ax = b 의 유일한 행공간의 해
x의 항목들은 선형결합 b를 얻기 위해 열벡터에 곱해지는 가중이다.
영공간이 있고, A의 행공간과 같은 영공간의 직교여공간이 있다.
영공간의 임의의 원소와, 행공간의 임의의 원소로 R^n을 표현할 수 있다.

열공간의 원소인 임의의 벡터 b가 주어질 때
Ax=b의 해가 되는 유일한 행공간의 임의의 원소(r0)가 있다.
유일한 원소인가? r0 가?
행공간의 벡터 인 r1-r0 으로 계산해보자. 사실 이것은 영공간의 벡터이다. 가능한 것은 영벡터 뿐이다.
즉, r1 = r0 인 것이다.
Ax = b 에 대한 해는 r0(행공간의 원소)과 n0(영공간의 원소)의 합으로 쓸 수 있다.

해인 x의 길이를 제곱해보자. 이것을 풀어보면
x의 길이의 제곱 = 행공간의 원소 길이 제곱 + 영공간의 원소 길이 제곱
이것은 행공간의 길이의 제곱보다 크거나 같다.
Ax=b 의 해는 r0보다 크거나 같다.

정리하자면, b가 A의 열공간의 원소라면, A의 행공간의 원소인 고유한 r0이 존재한다.
r0은 Ax=b에 대한 해이다.
r0은 가장 작은 해이다. 그 어떤 해도 r0 보다 작은 길이를 가질 수는 없다.
A의 열공간의 원소인 임의의 벡터 b가 존재한다면,
가장 작은 해가 행공간의 고유한 원소로 존재한다.
Ax = b의 행공간 해 예제
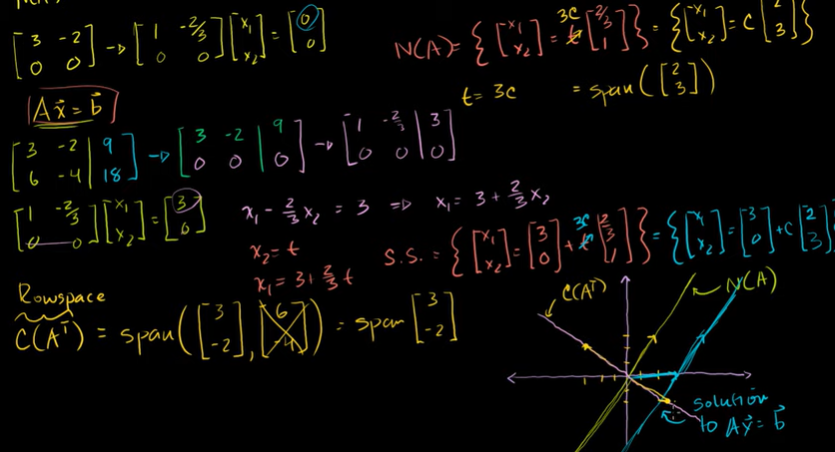
영공간의 직선, 해의 집합의 직선, 행공간의 직선
행공간의 벡터 중에서 해의 집합과 닿는 벡터가 있다. r이라고 하자.
해의 집합의 원소를 가리키는 행공간의 유일한 벡터이다.
해의 집합을 사방으로 닿을 수 있지만 해의 집합에 이르는 가장 짧은 것은 초록색 선이다.
벡터 [3 0] 에서 r = c[3 -2]을 빼면 영공간에 속하는 벡터(핑크색)를 찾게 된다.
이것과 행공간에 있는 벡터는 직교하기 때문에 내적하면 0이 된다.
이를 풀어서 c를 찾을 수 있다.
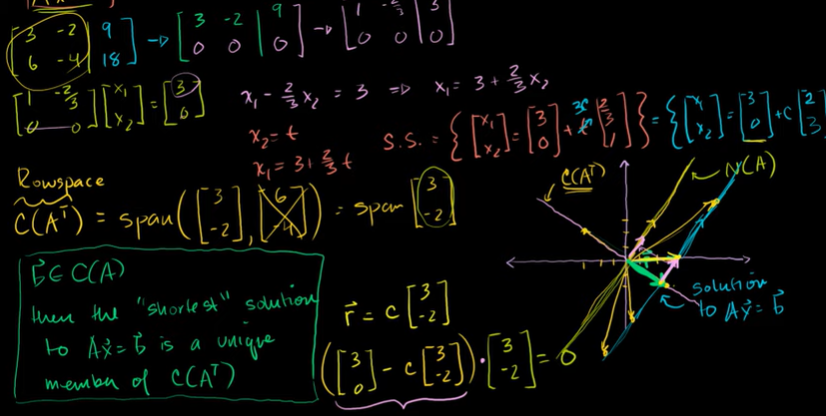
2. 정사영
부분공간에 대한 정사영
부분공간에서 직선에 대한 정사영은 이미 학습한 바가 있다.
임의의 부분공간에 대한 정의로 확장할 수가 있다.
v 벡터는 부분공간 V에 대한 정사영이고, w는 V의 직교여공간에 대한 정사영이다.
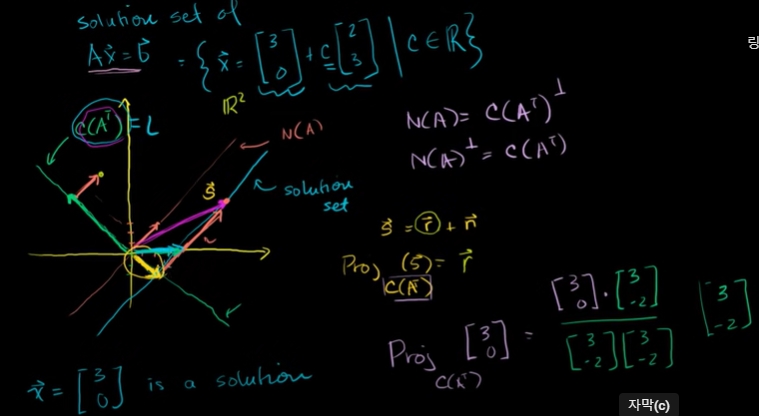
행공간의 특정 원소와 영공간의 특정 원소의 합으로 공간을 나타낼 수 있다.
해집합의 임의의 해를 갖게 된다.
행공간의 원소이기도 한 이 해집합의 어떤 원소는 가장 길이가 짧은 해가 된다.
임의의 해를 행공간에 정사영하면 노란색 벡터가 된다.
여기서는 부분공간이 직선이다. 직선인 경우가 대다수다.
행공간에 대하여 벡터 [3 0]을 정사영한 것이다.
평면에 대한 정사영 시각화
w는 L의 직교여공간 위의 고유 벡터이다. L에 있는 모든 벡터와 직교해야 한다.

평면에서 , x의 V에 대한 정사영은 V에 있는 어떤 고유 벡터이고
x - w('x의 V에 대한 정사영') 은 V에 있는 모든 벡터와 직교한다. (=v)
벡터v는 부분공간 V에 대한 벡터 x의 정사영이다.
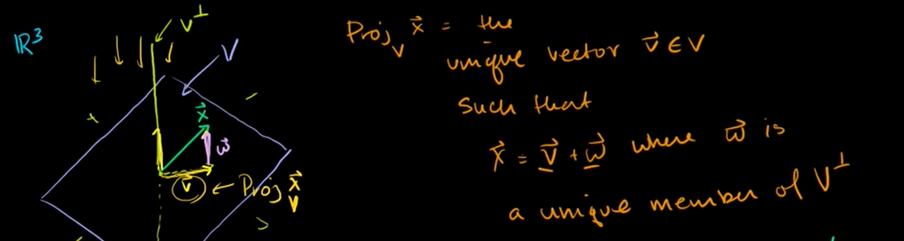
부분공간에 대한 정사영이 선형변환이라는 것 확인하기
k개의 기저벡저가 있고 이는 V를 이루는 기저이다.
부분공간의 원소인 임의의 벡터 a가 이들의 선형결합으로 표현될 수 있다.
A라는 행렬을 만든다고 했을 때 열은 부분공간의 기저벡터이다.
n개의 행을 가진다.
부분공간 V의 임의의 원소가 이들의 기저벡터의 선형결합으로 표현될 수 있다는 것은
부분공간 V의 임의의 원소 a가 행렬 A와 벡터 y 의 곱으로 표현될 수 있음을 나타낸다.
부분공간의 임의의 원소는 행렬 A와 R^k의 임의의 벡터의 곱으로 나타낼 수 있다.
V로 투사되는 x는 부분공간 V의 원소가 된다. Ay로 표현할 수 있다.
즉 Ay 에서 R^k에 존재하는 임의의 벡터 y와 같다.
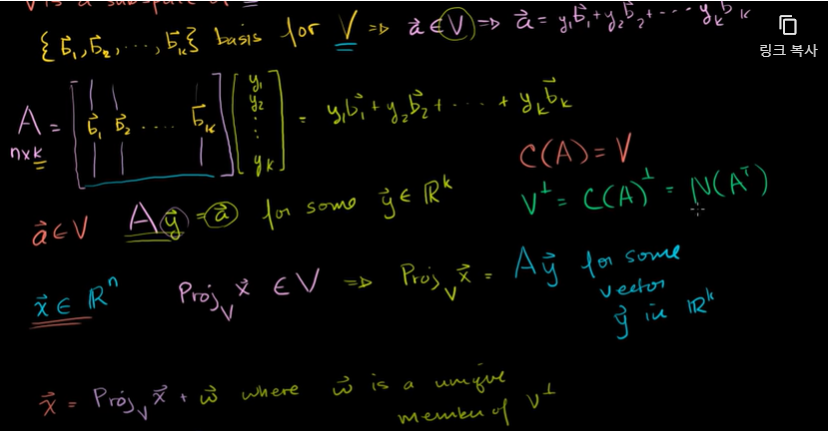
투사의 정의
x = v로 투사되는 x + w (v의 직교여공간)
A의 열공간은 V와 같다.
V의 직교여공간은 열공간의 직교여공간 즉 좌영공간(전치의 영공간)과 같다.
A의 전치를 이것과 곱하면 영벡터가 된다. 이것이 영공간이다.

x의 V에 대한 투사를 알 수가 있다. 정사영을 알 수 있는데 투사를 위한 변환행렬을 구할 수가 있다.
어떻게 활용할 수 있을까?
3차원 그래픽에서 물체가 임의의 관측자의 시선(임의의 부분공간)에서 어떻게 보일지 구하는 것이다.
부분공간의 기저를 안다면 변환을 적용할 수 있다.
부분공간 정사영 행렬의 예제
부분공간에 존재하는 다른 변환행렬을 알 수 있다.
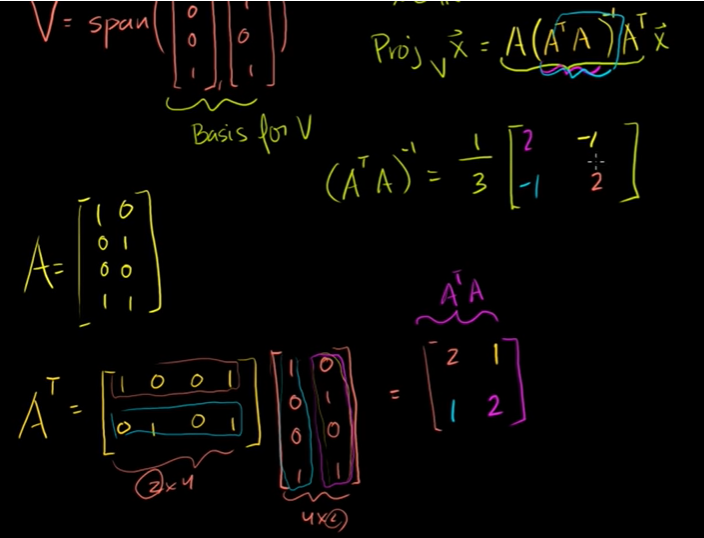

정사영 행렬의 다른 예제
R3 에 있는 어떤 벡터 x의 V에 대한 투영 행렬의 변환행렬
3차원의 방정식을 가지고 기저 벡터를 구할 수 있다.
x는 부분공간 V에 속한 벡터 v의 일차결합과 직여공간에 속한 벡터 w의 합으로 구할 수 있다.
이것을 정사영한 것으로 구할 수도 있다.
x를 V에 투영한 벡터와 V의 직교여공간에 투영한 벡터의 합으로 구할 수 있다.
3차 항등행렬 = V에 대한 투영행렬 + V의 직교여공간에 대한 투영행렬
V의 직교여공간에 대한 투영행렬을 구해보자
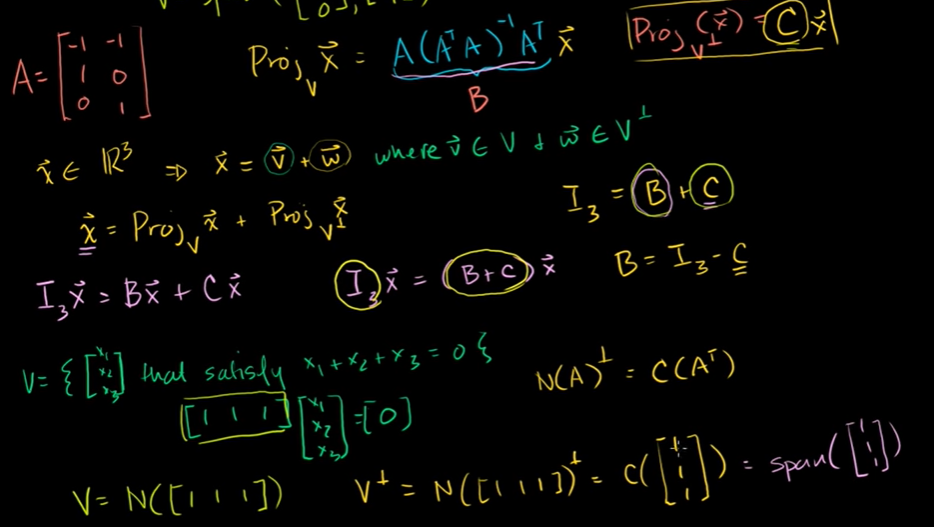
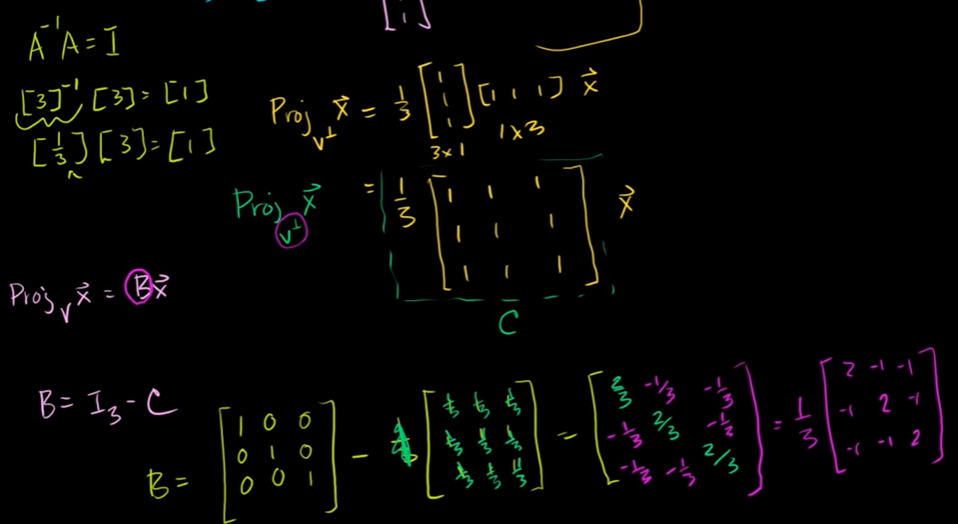

정사영은 부분공간에서 제일 가까운 벡터라는 것을 확인하기
x와 x를 부분공간으로 투영한 벡터(정사영)간의 거리가 제일 가깝다?
x-v = b+a
V 내의 다른 벡터들과 R3에서 임의로 고른 벡터인 x와의 거리보다 더 가깝다.
||x - v|| > ||a||
최소제곱 근삿값
해가 존재하지 않는다는 것은
선형결합에서 b를 나오게 만드는 a의 열벡터에 가중치가 없다는 말이다.
다른 말로, a의 열벡터의 어떤 선형결합도 b와 같지 않을 것이다.
b가 a의 열공간에 존재하지 않는다.

해가 존재하지 않는 것을 찾기 위해서는 0 = 1과 같은 식을 도출하곤 했다.
조금 더 간편하게 가장 해와 가까운 답을 찾을 수 있을까?
b - Ax를 최소화해야 한다.
b를 C(A) 열공간에 투사한 벡터가 최소이다.
Ax - b 는 C(A)의 직교여공간(=좌영공간)에 포함된다.
Ax = b 의 해가 존재하지 않는다.
b와 Ax의 거리를 최소화하는 x를 찾아보면 이것이 가장 작은 제곱 해이다.
그러려면 Ax가 A의 열공간(C(A))에 투사된 b가 되어야 한다.
Ax - b 를 쉽게 계산하려면 A의 전치를 양쪽에 곱해준다.
이 식은 항상 해(x)가 존재할 것이고 그것이 가장 작은 제곱의 해가 된다.
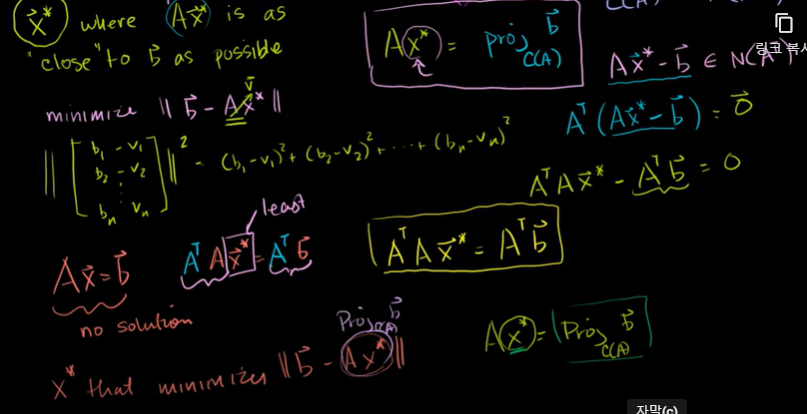
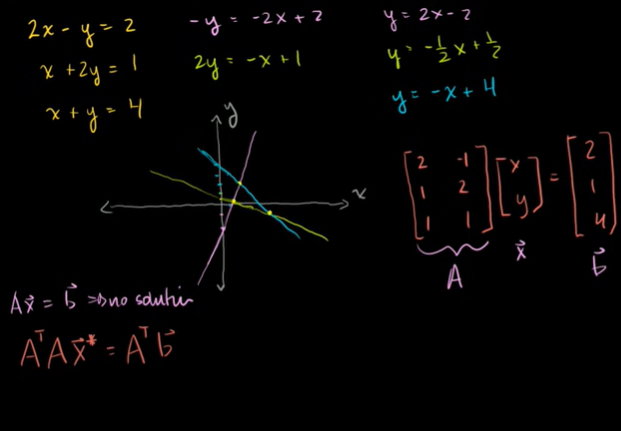
최소제곱 예제
세 개의 직선이 만나는 지점, 즉 해가 없다.
최고제곱근 해는 최고의 추정치이다.
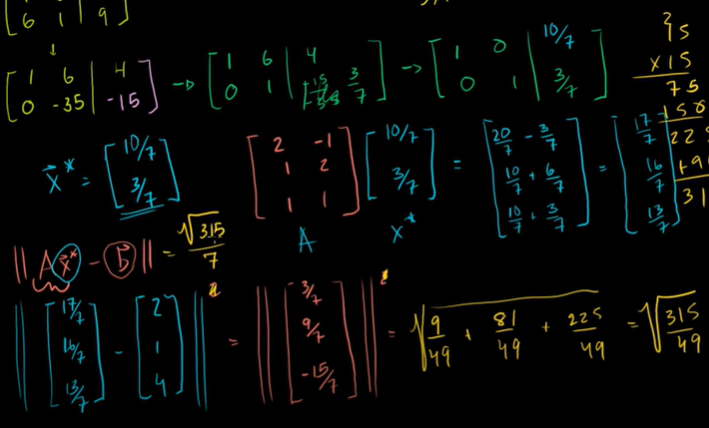
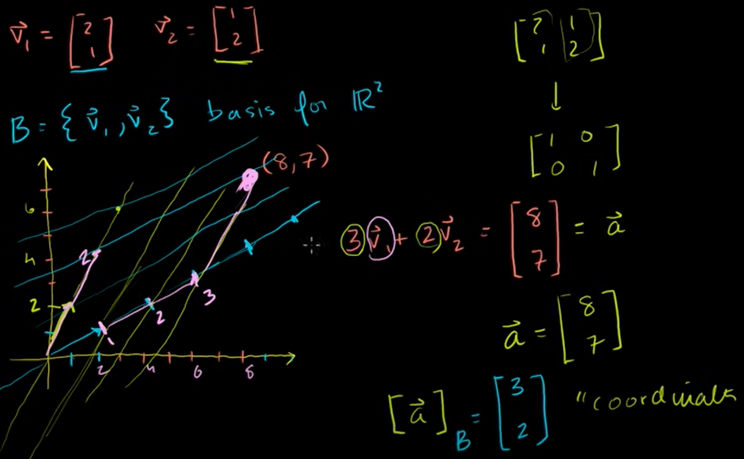
3. 기저변환
기저에 대한 좌표
기저 B에 대한 벡터 a는 가중치들과 기저벡터들의 결합이다.
문자 그대로 v1 방향으로 얼마 만큼, v2 방향으로 얼마 만큼 가는지 표현한다.
우리가 흔히 쓰던 좌표는, 사실 표준기저와 관련된 것이다.
e1 = [1 0], e2 = [0 1] 이다.
기저변환행렬
C는 기저벡터들로 이루어진 행렬 (=기저변환행렬)
기저 B에 대한 벡터 a의 좌표
이 두 개를 곱하면 벡터 a가 나온다.
표준 표현이나 표준기저에 대한 좌표가 있으면 엄청 쉽다.
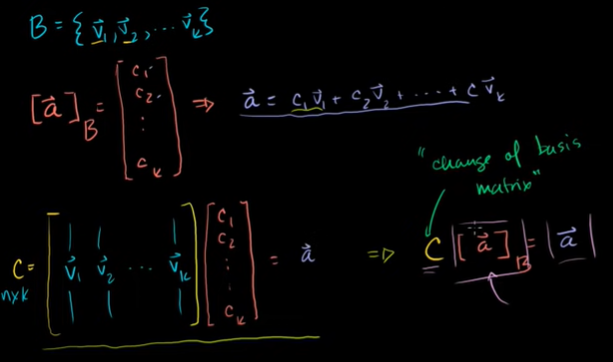
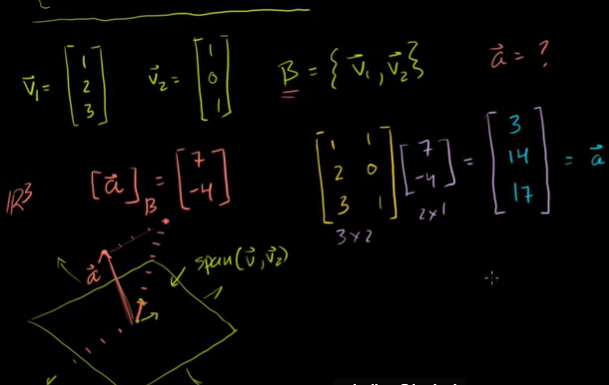
가역성이 있는 기저변환행렬
기저변환행렬은 열들에 기저 벡터들로 구성된 행렬이다.
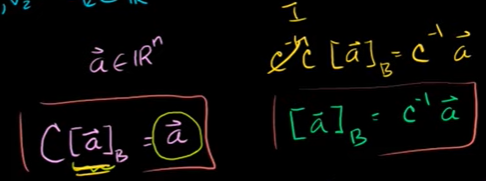
C의 역행렬이 있다고 가정해보자.
즉, 정사각행렬이자 행이나 열이 선형독립한다는 것이다.
C의 역행렬이 존재하면, 기저벡터의 선형결합을 이용하여 Rn의 그 어떤 벡터도 만들 수 있다.
기저 B의 생성은 nxn 이므로 R^n과 같게 된다.
표준 좌표와 기저에 관한 자표로 번갈아 표현할 수 있게 된다.
식의 양쪽을 C의 역으로 곱해준다.
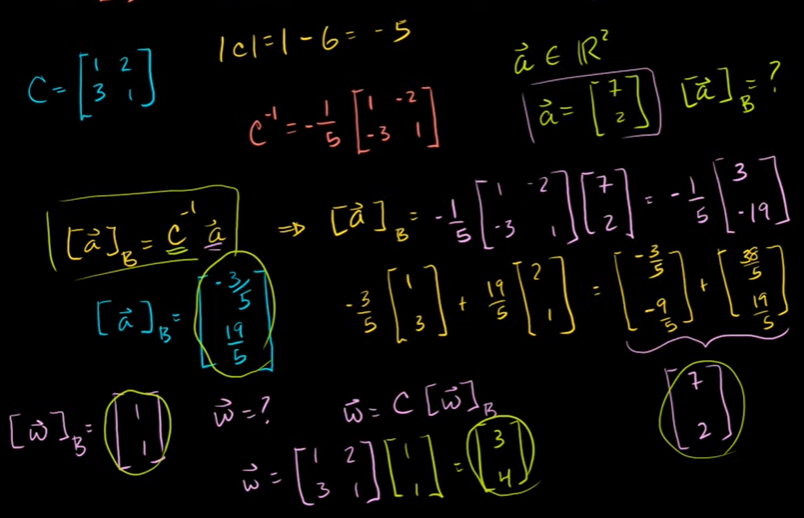
기저에 대한 변환행렬
선형변환 T(x)가 있을 때 이것을 Ax 라고 표현할 수 있다.
A는 T를 위한 변환행렬이다.
x라는 표준기저에 관해서 있을 때만!
공역에 존재하는 x의 사상을 B에 관한 좌표로 표현할 수 있다면
이것은 다른 행렬과의 곱으로 표현할 수 있다. 여기서 쓰이는 행렬을 D라고 해보자.
결국 이것은 B에 관한 좌표로 표현되는 x의 변환과 같다.
이 선형변환은 Ax이다.
양쪽을 C의 역행렬로 곱하면 간소화할 수 있는데
x는 'C X 비표준좌표로 표현된 x'와 같다.
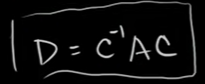
D가 기저 B로 표현되는 T를 위한 변환행렬이라면
C가 B를 위한 기저행렬의 변화라면
A가 표준기저로 표현되는 T를 위한 변환행렬이라면
행렬 D = C의 역 * A * C

번갈아 생기는 기저의 변환행렬 예제


위에서 한 모든 것의 정리이다.
A와 D 모두 변환이다. 단지 다른 좌표계에서 행한다는 것만 다르다.
다른 좌표계는 같은 벡터를 나타내는 다른 방법이다.

기저변환을 하는 변환행렬이 왜 중요할까?
선형대수학은 알맞은 기저를 고르는 학문이다. Art of choosing the right basis
A같은 행렬을 여러번 반복하면 복잡한 숫자가 된다.
기저들을 변환하면, 즉 B같은 기저나 D같은 대각행렬로 변환하면 곱하는 것은 상당히 간단해진다.
알맞은 좌표계를 선택하면 많은 문제들의 연산이 쉬워진다.

좌표계 변환을 이용한 변환행렬 구하기
D의 첫번째 열은 B좌표로 된 첫번째 기저벡터에 적용된 변환이다.
v1의 변환은 L을 기준으로 반대편으로 넘어가서 '-'가 붙는다.
v2의 변환은 L 선상에 있기 때문에 그대로이다.
이렇게 구하면 D를 훨씬 쉽게 구할 수 있다.
이를 통해 A까지 구할 수 있다.
변환행렬 D를 기저좌표계에서 먼저 찾고, 표준기저에 대해 변환행렬 A를 찾는 게 더 쉽다.

4. 정규직교기저와 그람-슈미트 과정
정규직교기저란?

정규직교집합 : 모두 정규화 되었으며, 서로에 대해 직교한다.
[ortho normal basis]
정규화되었다는 것은 모든 원소가 길이 1을 지닌다.
다른 벡터끼리 내적하면 직교하기 때문에 0이 나오고,
자기 자신과 내적하면 길이의 제곱이기 때문에 0이 나온다. (우측 그림)
동시에 선형 독립이다.
정규직교집합이 있다면, 선형독립인 벡터들의 집합이면서, 부분공간의 기저가 된다.
정규직교기저에 대한 좌표
정규직교기저는 좋은 좌표계를 만든다.
x를 선형결합으로 만든 다음에 vi 를 모두 곱해주면 다음 식을 얻을 수 있다.
vi · x = ci
x를 기저 B에 대해 나타내면 각 좌표는 서로 다른 기저 벡터들의 계수가 된다.
가역성이 있는 경우에 이것은 C의 역행렬로 나타낼 수가 있었다.
그런데 가역성이 없는 경우는 어떻게 해야 할까?
이럴 때 위 식을 이용해서 x를 기저 B에 나타낼 수 있다.
보통은 기저변환행렬을 이용해서 구할 수 있다.
그런데 정규직교기저에서는 보다 쉽게 구할 수 있는 것이다.
기저에 대해 좌표를 구하는 것이 훨씬 쉽다.
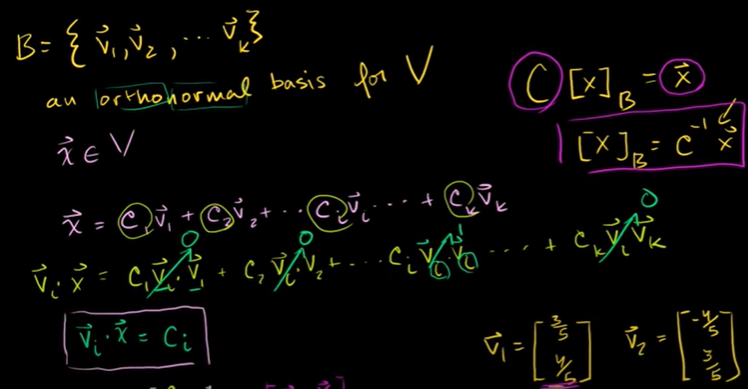
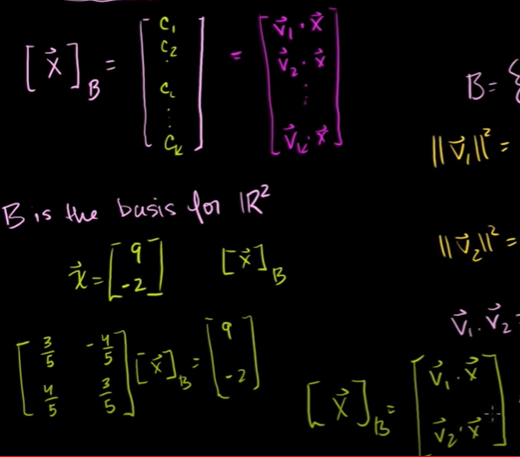
정규직교기저를 이용한 부분공간에 대한 정사영
R^n 의 원소 x = 부분공간의 벡터 v + 부분공간의 직교여공간 내의 벡터 w
v는 x를 V에 투영한 것으로 표현한다.
전에 배운 것처럼 이것은 오른쪽에 있는 식처럼 복잡하게 계산했다.
그런데 동시에 기저벡터들의 선형결합으로 표현할 수도 있다.
ci 를 각각의 기저벡터들과 곱하는 것과 같다.
정사영이 선형 변환이다. 이것이 얼마나 더 편리할까?
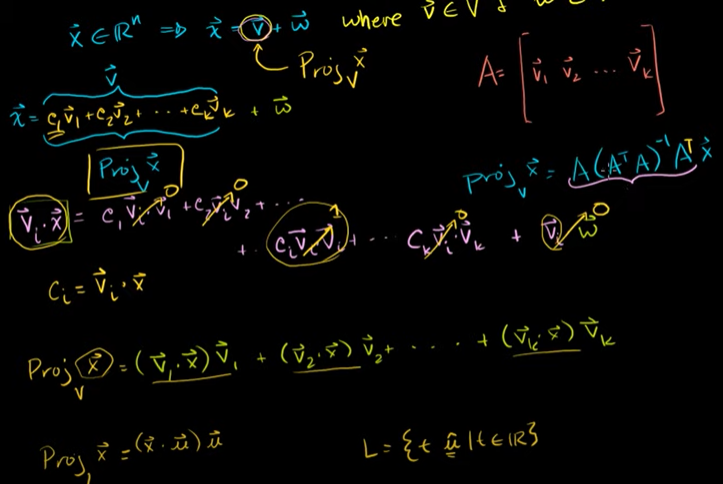

정사영을 구하는 방법
기저벡터와 x를 내적한 값이 계수가 되며, 각 계수와 기저벡터를 곱한 것들을 더한다
정규직교집합이면 식에서의 과정이 단위행렬이 되면서 간소화된다.
예제

변환행렬을 찾기 위한 직교기저변환행렬을 이용하는 방법의 예제
C^-1 * C = In
nxn 행렬에서는, C^T * C = In
nxn 행렬이 정규직교집합을 형성할 때 C의 역행렬이 C의 전치행렬과 같다.
언제 유용하냐면.. 10차원의 역행렬을 찾는 것은 시간이 정말 오래걸리지만, 전치행렬은 쉽게 찾을 수 있다.
v1과 v2는 평면 상에 있기 때문에 변환해도 그대로지만, v3는 직교해 있기 때문에 마이너스가 붙는다.
T(X) = Ax 에서 A를 구하기가 어렵다면 둘러서 갈 수 있다. 이렇게 A를 구할 수 있다.
nxn 행렬이 정규직교집합을 형성한다면 C의 역행렬을 C의 전치행렬로 바꿀 수 있다.

D를 구하는 것은 B좌표로 된 기저벡터에 적용된 변환을 이용하면 된다. 각각의 변환은 미리 알아봤다.
최종적인 값은 v1, v2 두 벡터에 의해 생성되는 평면에 반사되는 변환을 이 행렬로 나타낼 수 있다.
A값을 구했기 때문에 T(X) = Ax 를 표현할 수 있다.
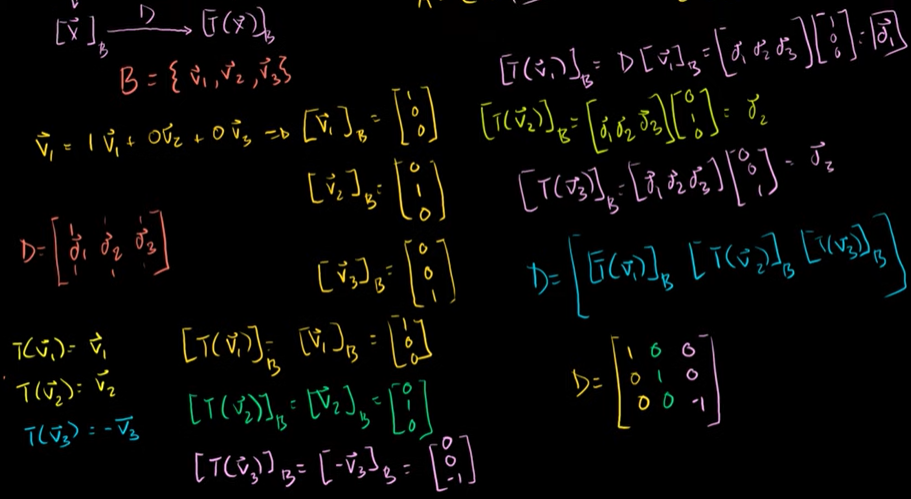
각도와 길이를 보존하는 직교행렬
기저변환행렬 혹은 직교행렬에 의한 변환은 각도와 길이를 보존하면서 벡터가 뒤틀리지 않는다.
벡터들을 회전시키거나 이동시킬 수는 있지만 뒤틀지 않는다.
그람-슈미트 과정
정규직교기저를 만드는 과정을 그람-슈미트 과정이라고 한다.
1차원 부분공간 V1의 기저가 벡터 v1이라고 해보자.
어떻게 이 벡터를 정규직교하게 만들 수 있을까?
벡터가 하나이므로 다른 모든 벡터와 직교한다.
길이를 1로 만들려면 v1 을 v1으로 나눠주면 된다.
2차원 부분공간 V2의 기저가 v1, v2 라고 해보자.
벡터 v1은 벡터 u1의 일차결합이라고 볼 수 있다. 따라서 기저를 생성할 때, u1과 v2로 표현할 수 있다.
v1과 v1의 직교여공간 벡터를 더하면 v2 를 구할 수 있다.
이렇게 보면, x는 v2의 v1에 대한 정사영이기도 하다.
결국, y2(v1의 직교여공간 벡터) = v2 - x(v2의 v1에 대한 정사영)
u1과 y2의 결합으로 v2를 만들 수 있다.
그래서 V2 집합은 u1과 y2 두 기저벡터로 생성될 수 있다.
이 두 벡터는 직교한다.
y2 역시 y2로 나누어주면 길이를 1로 만들 수 있기 때문에 정규직교기저를 만들 수 있다.

V3는 어떻게 정규직교기저로 바꿀 수 있을까?
u1, u2, v3 로 이루어졌다.
다른 벡터와 일차결합하여 v3를 충분히 나타내면서 u1, u2와 직교하는 새로운 벡터를 구해야 한다.
y3를 구하면 u1과 u2의 일차결합으로 구할 수 있다.
벡터 v3의 부분평면 V2에 대한 정사영을 구한다.
y3 = v3 - v3의 정사영
정사영은 '정규직교기저를 이용한 부분공간에 대한 정사영'에서 배운 것처럼 변환할 수 있다.
u3를 y3에서 y3의 길이로 나누면 길이를 1로 맞출 수 있다.

그람-슈미트 과정 예제

5. 고유값, 고유벡터, 고유공간
고유값과 고유벡터란?
벡터는 크기만 바뀌거나 방향만 뒤집히게 된다. 변환에 의해 확대되거나 축소되는 벡터.
벡터들의 방향이나 이들이 생성하는 직선은 변하지 않는다.
T(v) = λ v 을 따르는 벡터들을 변환 T에 대한 고유벡터(eigenvector)라고 부른다.
고유벡터에 곱해지는 람다( λ ) : 고유벡터에 대응하는 고유값(eigenvalue)이라 합니다
고유값을 결정하는 식 증명
벡터에 항등행렬을 곱해도 그 자신을 의미한다.
행렬 벡터 곱은 분배법칙이 성립한다.
어떤 행렬 벡터곱이 0과 같다는 것을 나타낼 수 있다.
v가 행렬의 영공간의 원소이다.
영공간에 영벡터 이외의 원소가 존재해야 한다.
D의 열들은 D의 영공간이 영벡터를 지니는 경우에 대해서만 서로 선형독립이었다.
행렬이 영공간에 영벡터 외의 원소를 지니기 위해서는 선형종속인 열들을 지녀야 한다.
λ In - A 가 선형종속인 열들을 지녀야 한다.
가역성을 지니지 않기 때문에 행렬식이 0이다.
0이 아닌 v에 대해 Av = λ v가 되기 위한 필요충분조건은 ' λ In - A의 행렬식'이 0이 되어야 한다.

2x2 행렬의 고유값을 구하는 예제
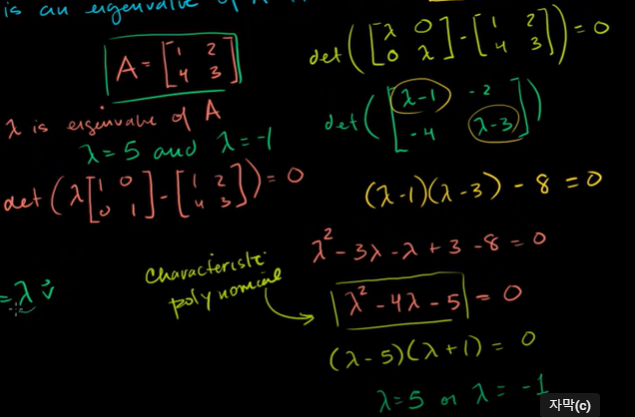
고유벡터와 고유공간을 구하는 예제
어떤 고유값 λ 에 대해 λ 에 대응하는 고유벡터들의 집합을 λ 에 대한 고유공간이라고 한다.
이 벡터들의 집합은 이 행렬의 영공간이다.
고유값 5와 -1에 각각 대응하는 영공간을 찾아서 고유벡터들을 찾을 수 있다.
벡터를 표준 위치에 그릴 때 고유벡터에 대응하는 고유값은 늘 동일할 것이다.
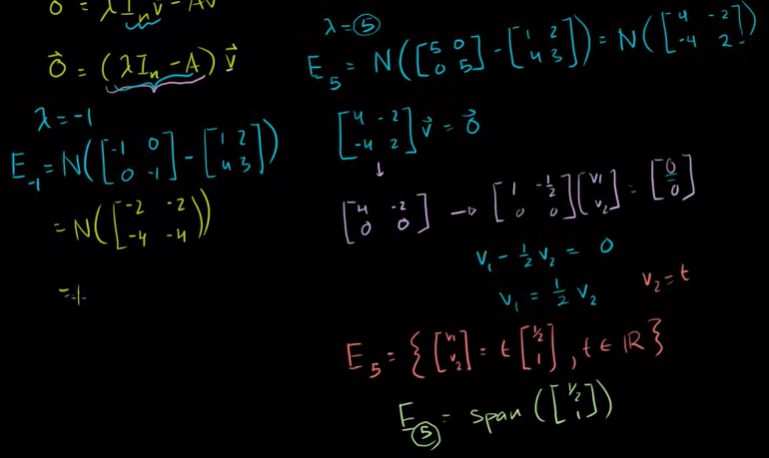

3x3 행렬의 고유값
λ 는 A의 고유값이다.
사루스 법칙을 통해 λ 에 대한 행렬식을 나타낼 수 있다.
행렬의 행렬식을 0으로 만드는 람다 λ 가 해이다.
3x3 행렬의 고유벡터와 고유공간
고유값을 행렬에 집어넣어 이것이 벡터와 곱해 0이 나오는 영공간을 찾아야 한다.
λ = 3에 대응하는 두 벡터의 생성인 고유공간을 그릴 수 있다.
λ = -3에 대응하는 한 벡터의 생성인 고유공간은 직선이다.
벡터는 Ax가 되면서 위 고유공간에서는 3배 길어지고 아래 고유공간에서는 3배 반대로 길어진다.
고유기저와 좌표계
벡터 v1의 변환(T(v1)) = A v1 = λ v1
벡터 v1이 A의 고유벡터이므로 이는 어떤 고유값 λ1과 벡터 v1의 곱과 같다.
이것을 영벡터들과의 합으로 나타낼 수 있다.
이를 통해 이들을 기저로 사용하여 이 기저들을 기준으로 한 좌표를 구할 수 있다.
기저벡터의 계수를 구할 수 있다.
기저변환을 진행하면 여러번 계산을 할 때 유용할 수 있다. 계산하기 쉬운 대각행렬이 구해질 수 있다.
새로운 기저에 대한 변환행렬을 구할 수 있다.
기저는 n개의 선형독립인 고유벡터로 정의되며 행렬 A의 고유벡터였다.
A의 선형독립인 고유벡터를 기저로 사용할 때, 이를 고유기저라고 한다.
고유기저로 나타낸 변환행렬 D는 유용하다.
곱하기 쉽고 역행렬과 행렬식 모두 쉽다. 다루기 쉬운 기저이다.
고유기저가 좋은 기저벡터를 만들 수 있다.
고유벡터와 고유값을 이용해 기저를 변환시켜서 문제들을 더 간단하게 풀 수 있다.

'Mathematics and Statistics' 카테고리의 다른 글
| Review >> Essence of Linear Algebra_3Blue1Brown (1) | 2024.01.14 |
|---|---|
| Essence of Linear Algebra_3Blue1Brown (2) | 2024.01.14 |
| Review >> Linear Algebra_Khan (2) | 2024.01.09 |
| Linear Algebra_Khan [2/3] 행렬변환 (2) | 2024.01.03 |
| Linear Algebra_Khan [1/3] 벡터와 공간 (1) | 2023.12.28 |
