1. 함수와 선형변환
함수 더 이해하기
함수는 한 집합에서 다른 집합으로 가는 변환이다.
대응시키려고 하는 집합은 정의역이다. (domain)
대응되는 집합 대상은 공역이다. (codomain)
공역은 대응 대상이 될 가능성이 있는 집합이다.
치역은 공역에서 함수가 값을 대응시키는 부분의 부분집합이다. (range)
R이나 R의 부분집합에 대응시키는 1차원 함수는 실수값함수 또는 스칼라값함수이다.
1차원 공간보다 높은 차원의 공간이나 부분 공간에 대응시키는 함수는 벡터값함수이다.


벡터의 변환
함수 f는 R^3안의 벡터를 R^2안의 벡터로 대응시켜준다.
변환(transformation)을 하게 되면 함수 f 를 T 로 바꿔서 많이 표현한다.
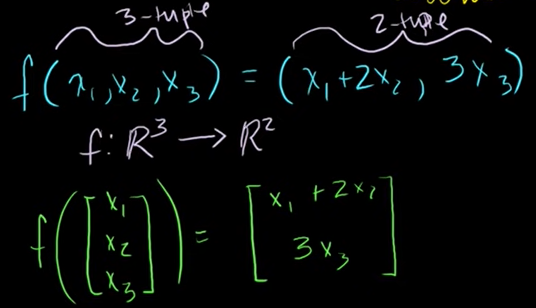

선형변환

Linear Transformation
다음과 같은 필요충분조건이 있다.
선형변환인지 아닌지 직관적으로 알고 싶다면 그 성분이 다른 성분들의 선형결합만을 포함한다면 선형변환이다.
성분이 서로 곱해지거나 제곱이나 지수가 있다면 선형변환이 아닐 가능성이 크다.
선형 변환의 행렬벡터적
행열의 곱 또는 행열 벡터적은 항상 선형변환이다.
Matrix product with vectors is always linear transformation

행렬 벡터적의 선형변환
단위행열은 각 행벡터에서 하나만 1을 가지고 나머지는 0이다.
이 벡터에 다른 벡터를 곱하는 것으로 사용할 수 있다.
하나의 행벡터마다 e1, e2, ..., en 이라고 부를 때, R^n의 표준기저(standard basis)라고 부를 수 있다.
기저이기 때문에 Rn을 생성해야 하고, 선형독립이어야 한다. 생성의 조건을 만족하려면 이 벡터들의 선형결합식이 어떤 벡터라도 표현할 수 있어야 한다.
따라서, 모든 선형변환들이 행열과 벡터의 곱으로 표현될 수 있다.
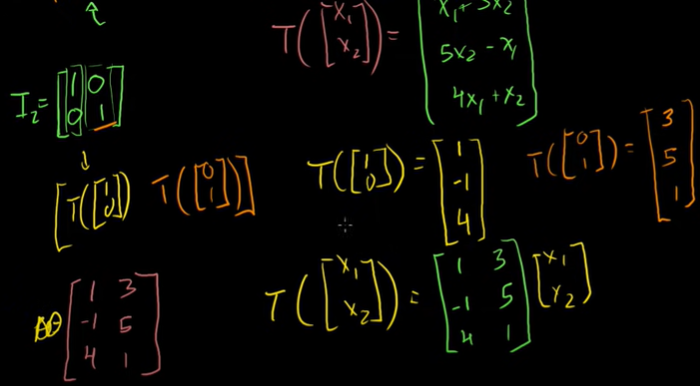
변환에서의 부분집합의 상
세 가지의 선분 방정식을 세우면 삼각형을 만들 수 있다.
삼각형의 각 점들을 변환할 수 있다. 행열과 벡터의 곱으로 계산할 수 있다. 삼각형이 어떻게 될지는 모른다.
삼각형의 x0과 x1사이의 한 변인 L0의 변환은 종점들의 변환점들을 연결하는 선이다.
결국 선형변환을 통해 변경이 있더라도 간편하게 구할 수가 있는 것이다.
각각의 점들마다 변환된 값을 구할 필요 없이, 간단하게 종점들이 무엇인지 알아내고 변형을 찾아 변환된 점들을 연결하는 선을 찾으면 된다.
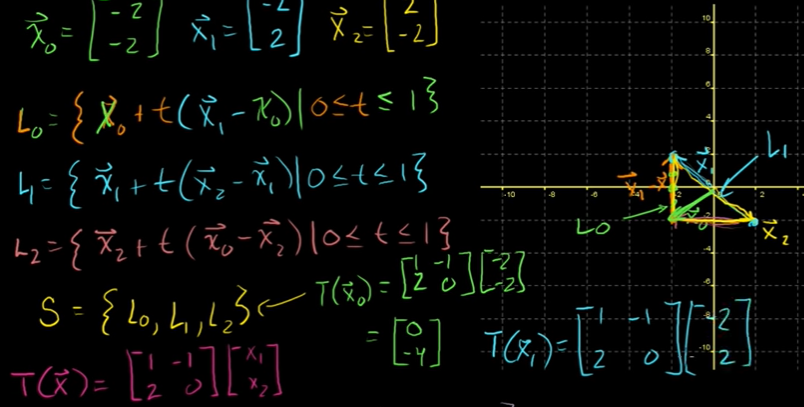
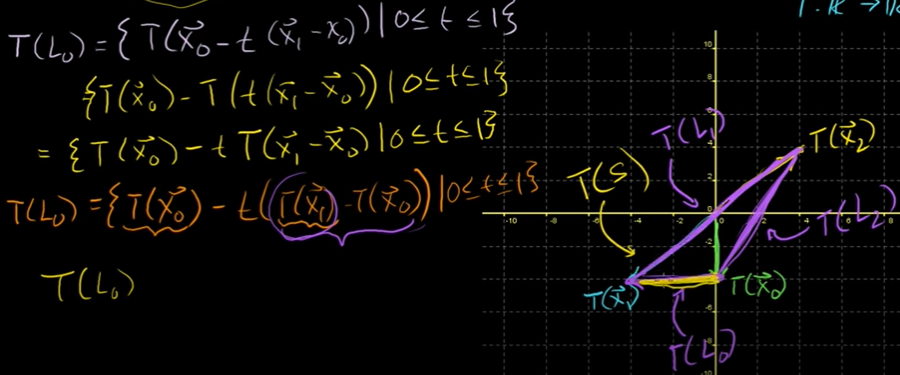
Im(T): 변환의 상
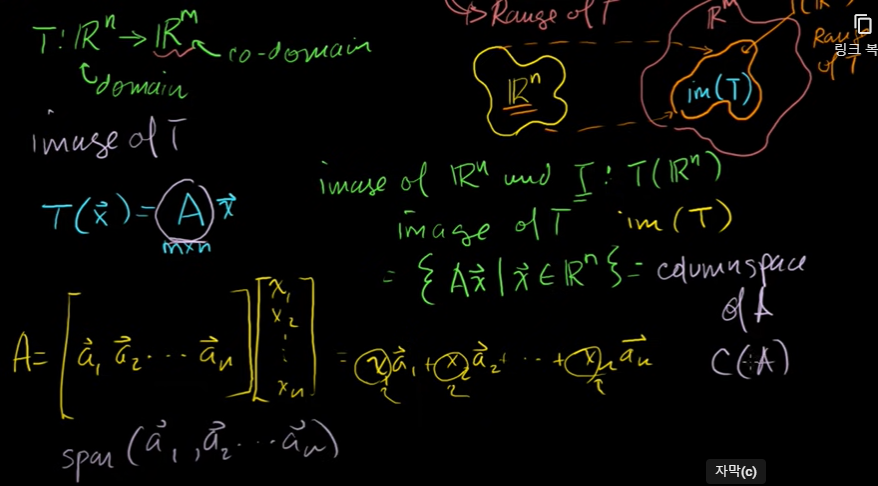
V 집합이 R^n의 부분공간이라는 가정.
이 부분공간을 변환시키면 어떻게 될까?
위의 삼각형을 예로 들자면, '오른쪽 삼각형은 image of 왼쪽 삼각형 under T' 이다.
모든 벡터들이 주어진 부분집합에서 T(V)는 부분공간이다.
Image of T (Im(T)) : T는 R^n에서 R^m으로 간다.
Image of R^n under T : T(R^n)
모든 선형변환은 행렬의 벡터적으로 표현할 수 있다.
모든 정의역의 원소들을 공역으로 사상하면 이건 선형변환의 상이다.
행렬의 열공간으로 변환을 표현할 수 있다.
열공간은 행렬의 열벡터들의 포괄하는 길이다.
집합의 원상
정의역이 아닌 반대로 공역 Y에서 시작한다면 어떨까?
정의역에 포함되는 벡터 중에서 부분집합 S에 대응하거나 변환되는 벡터의 집합을 구하면 된다.
모든 것이 대응하지는 않을 것이다.
원상: preimage of S under T
Q. 집합 S 의 원상의 상은? A. 집합 S의 부분집합이다.

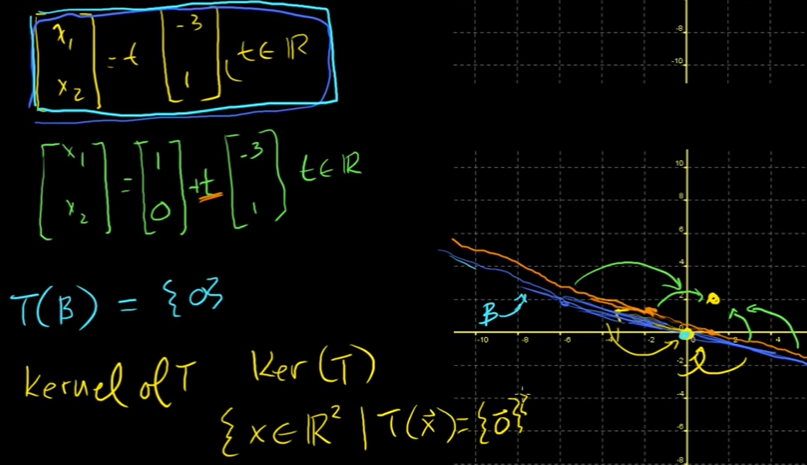
원상과 핵 예제


선형변환의 합과 스칼라 곱
x의 두 선형변환의 합을 행렬 벡터 곱으로 나타낼 수 있다.
행렬은 선형변형의 행렬을 합한 것이다.
행렬의 합과 스칼라 곱 심화
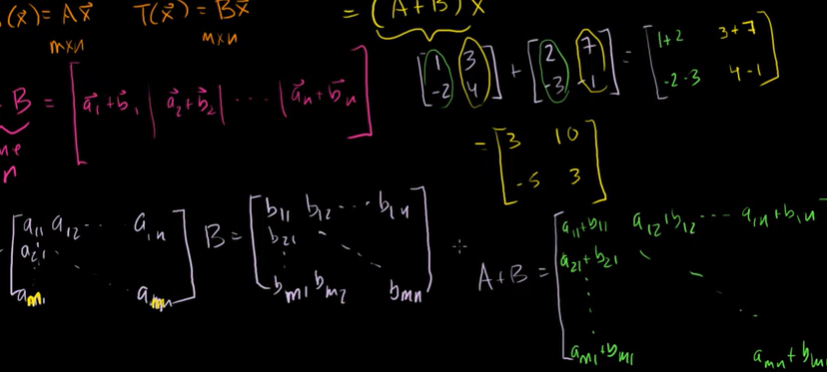
2. 선형변환 예제
스케일 변환과 반사
R2에서의 회전
회전변환을 행렬로 표현할 수 있다.
행렬을 찾으려면 단위 행렬에 변환을 적용해야 한다.
회전변환을 안다면 원하는 각도에 이 행렬의 값들을 구하고 그걸 위치벡터랑 곱하면 된다. 꼭짓점을 구하고 점들을 연결하면 회전하는 상을 구할 수 있다.

R3에서 x축을 중심으로 한 회전
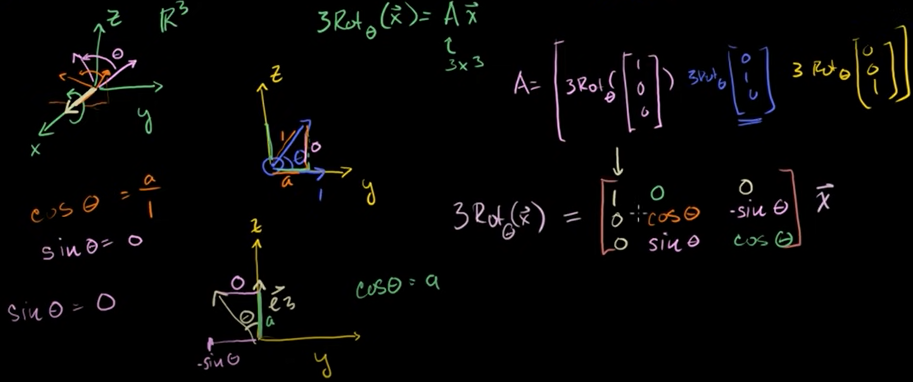
단위벡터
unit vector : 길이가 1인 벡터. vector has length of 1
u 가 단위벡터이고 R^n의 원소라면, u1부터 un까지 n 개의 길이를 가지고 있다.
길이는 각 성분의 제곱의 합의 제곱근이다.
어떻게 단위벡터를 만드는가?
v라는 벡터를 단위벡터인 u로 바꾸려면
단위벡터를 찾고 싶다면 R^n의 벡터 길이의 정의를 이용하여 v 의 길이를 구할 수 있다.
v라는 벡터를 v의 길이로 나눈다. 그러면 단위벡터를 구할 수 있다.
단위벡터의 경우에는 위에 화살표 대신에 꺾새 모양의 모자를 씌운다.

정사영

orthogonal projection
벡터 v 를 스칼라배하면 cv 벡터가 늘어날 수 있다.
원점을 지나는 직선. 벡터 x의 직선 L로의 정사영을 정의할 수 있다.
L에 놓인 x의 그림자로 볼 수 있다.
다르게도 표현할 수 있다. x가 L의 방향으로 얼마만큼 이동했는지 생각해볼 수 있다.
x에서 L로 가는 벡터는 수직이기 때문에 내적하면 0을 만들 수 있다.

행렬 벡터적으로 직선에 정사영 나타내기
벡터를 내적한 것은 벡터의 길이를 제곱한 것과 같다.
v벡터의 길이가 1이라면 단위벡터이다.
v의 가능한 모든 스칼라배는 v의 스칼라배인 단위벡터 u의 모든 스칼라배와 같을 것이다.
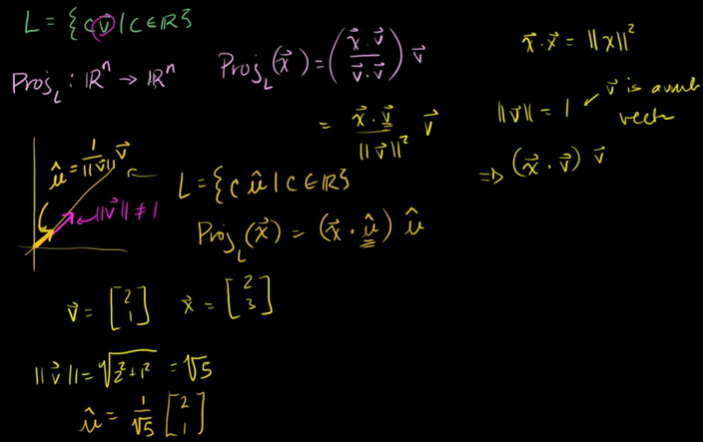
단위벡터를 이용하여 선을 재정의할 수 있다.
단위벡터로 바꾼 것이 R^n의 선 L에 대한 투영에서 선형변환의 조건에 부합하는지를 검증할 수 있다. 행렬 변환으로 바꿀 수 있다는 뜻이다. 어떻게 쓸 수 있을까?
L에 대한 투영을 할 때, L을 단위벡터 u의 임의의 스칼라배라고 해보자. 임의의 벡터 x를 L에 투영하면 행렬을 만들 수 있다. 이 행렬에 x를 곱하면 정사영(Proj(x))이 나오는 것이다.
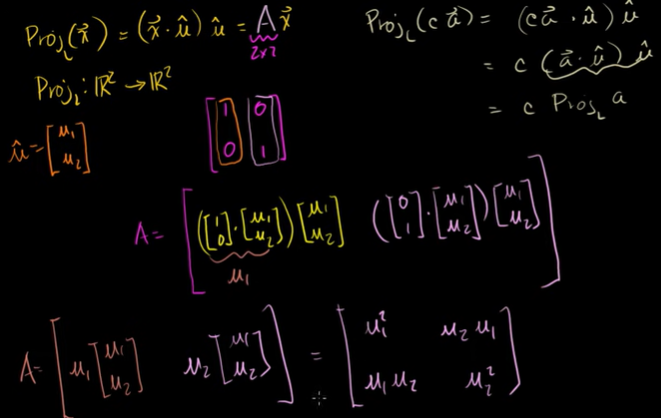
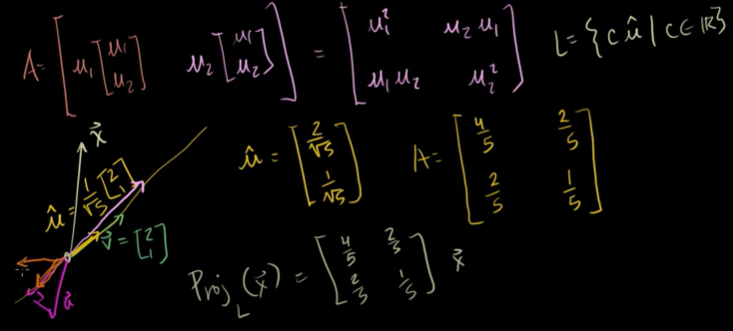
3. 변환과 행렬의 곱
선형변환의 합성
X에서 Z로 바로 가는 T와 S의 합성. composition
이것이 선형변환이 될 수 있을까? 조건을 부합하는지 확인해볼 수 있다.
덧셈과 스칼라배에 대하여 닫혀 있기에 이것은 어떠한 행렬에 벡터를 곱한 것이라고 볼 수 있다.
n 개의 열, l 차원의 공간으로 가는 것이다.
T o S (x) = B(Ax)
각각의 변환을 행렬로 바꾸려면 단위행렬로 바꾸어야 한다.

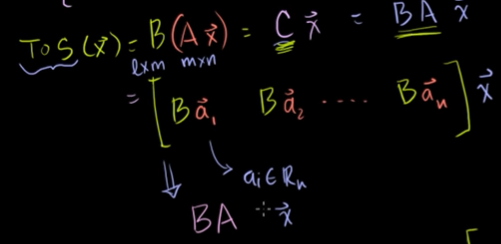
행렬곱 예제
벡터의 차수와 열의 수가 같아야 한다.
AB는 계산될 수 있지만, BA는 계산될 수 없다.
행렬끼리 곱하는 목적은 각각 행렬 A와 B로 나타나는 두 선형변환을 합성하기 위함이다.
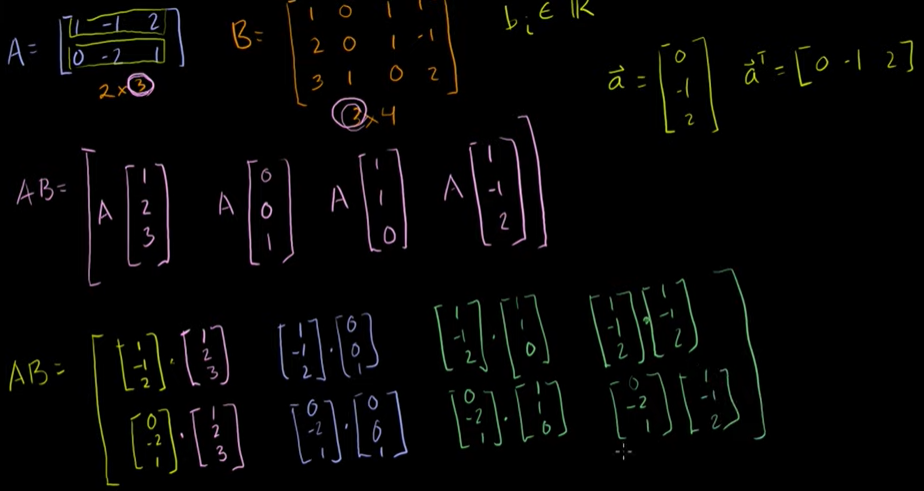
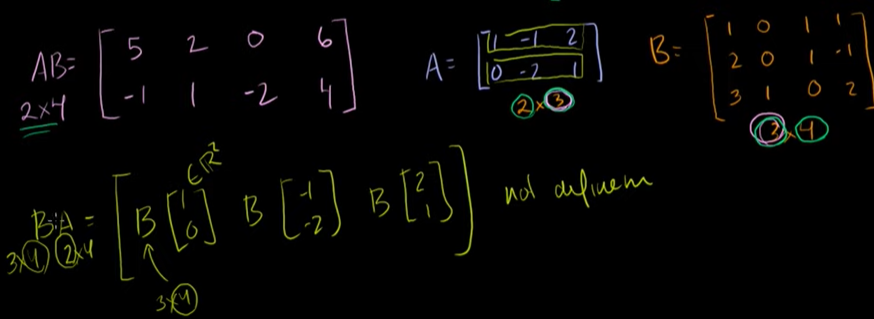
행렬곱의 결합법칙
괄호는 전혀 필요하지 않다.
단, 교환법칙은 성립하지 않는다.

행렬곱의 분배법칙
분배법칙은 행렬-벡터 곱셈에서 양방향 모두 성립한다.
하지만 둘이 같은 것은 아니다.
A (B+C) = AB + AC
(B+C) A = BA + CA
4. 역함수와 역변환
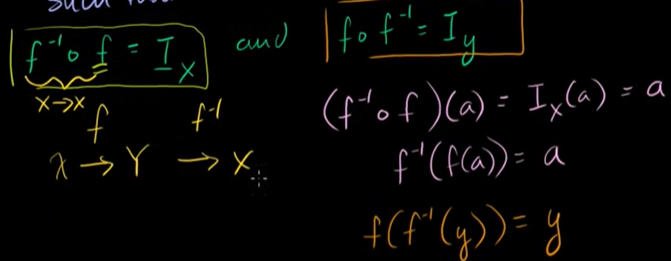
함수의 역이란?
항등함수는 원소를 그대로 뱉어낸다.
Ix(a) = a
f함수와 f의 역함수를 합성하면 항등함수가 나온다.
역함수가 되려면 두 가지를 만족해야 한다.
- 역함수와 함수의 합성함수는 X의 항등행렬이 되어야 한다.
- 함수와 역함수의 합성함수는 Y의 항등행렬이 되어야 한다.
어떤 함수든지 하나의 역함수만 가진다. 두 개의 다른 역함수를 설정할 수가 없다.
증명: 가역성은 f(x) = y 의 해가 유일함을 의미합니다.
집합 Y의 모든 원소 y에 대해 f(x) = y의 유일한 해가 존재한다면 f가 가역성을 지닌다는 뜻이다.
이 두 가지를 서로가 서로를 암시한다.
X에서 Y로 가는 함수가 가역적이면(역함수) ⇔(필요충분조건)⇔ 집합 Y의 모든 원소 y에 대해 f(x) = y의 유일한 해가 존재한다
전사함수와 단사함수
전사함수(surgective function) (onto)
공역에 있는 모든 원소 y에 대하여 집합 X에 적어도 하나의 x가 존재한다.
치역이 공역과 같으면 공역의 모든 값은 대응된 것이다. 전사함수인 것이다.
단사함수 (injective function) (one-to-one)
많아야 하나의 x가 대응한다. 대응되는 x가 없을 수도 있다. 하나를 넘을 수 없다!
가역성과 전사함수, 단사함수의 관계
서로 다른 2개의 x가 같은 y의 원소로 대응되면 그것은 일대일이 아니다. 단사함수가 아닌 것이다.
가역성을 지니기 위한 조건 ⇔(필요충분조건)⇔ f가 전사함수이고 단사함수이다.
변환이 전사함수인지 판별하기
변환과 함수는 본질적으로 같다.
공역의 모든 벡터를 열벡터들의 일차 결합을 통해 만들 수 있어야 한다.
전사함수가 되기 위해서는 행렬의 열벡터들인 행렬의 열공간으로 R^m을 생성해야 한다.
R^m 내의 모든 b에 대하여 해를 얻을 수 있어야 한다.
기약행사다리꼴을 만들어서 추축행들을 만들면 된다.
0으로 이루어진 행을 가지지 말아야 한다. 0이 되면 오른쪽 성분이 0이 되기 때문이다.
A의 계수(Rank(A)) = 열공간의 차원(dim(C(A))) = 열공간의 기저 벡터의 수
변환 T가 전사함수이기 위한 조건이 열공간 R^m에서 기약행사다리꼴행렬의 모든 행에 추축 성분을 가져야 한다는 조건과 필요충분조건이다.
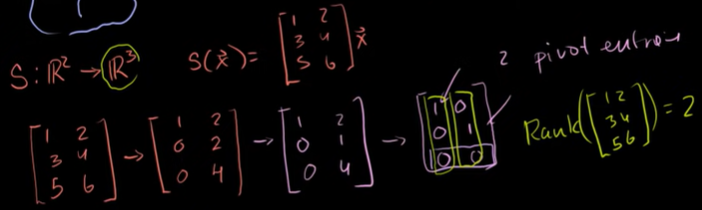
Rank(A) = m
Rank 가 2로 나왔는데 공역의 차원이 3이기 때문에 S가 가역성을 진지지 않는다는 것을 알 수 있다.
Ax = b의 해집합 구하기
해집합은 b가 해를 갖는 경우 어떤 b가 되는데 이는 공집합 혹은 영공간이 이동한 것과 같다.
단사변환에 대한 행렬의 조건
Ax = 0 을 세우고 0을 만족하는 모든 x를 찾는다.
단사함수라고 가정한다면 영공간이 영벡터만 가져야 한다. 그래야지만 하나의 해를 가지기 때문이다.
영공간이 영벡터를 포함한다면 모든 열들이 선형 독립이다. 이들은 열공간의 기저가 된다.
기저의 차원, 열공간의 차원은 기저를 형성하기 위한 벡터의 수와 동일하다. 계수가 n인 것이다.
따라서, 단사함수이기 위한 조건 ⇔(필요충분조건)⇔ 변환 행렬의 계수가 n이다.
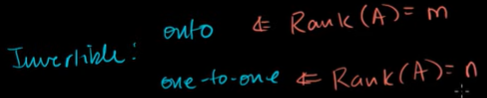
가역성의 조건을 간단히하기
A의 계수는 m과 같아야 하면서 n 과 같아야 한다. m=n 이다.
가역성을 지니기 위해서는 변환 행렬의 기약행사다리꼴의 형태가 n에 대한 단위행렬과 같아야 한다.
단위행렬이 n x n 형태가 되는 것이다.
rref (A) = In
역변환이 선형임을 확인하기

가역성을 지니기 위해서는 변환(함수의 다른 말)이 있을 때
T의 역변환과 T와의 합성이 정의역의 항등변환과 같고
T와 T의 역변환의 합성이 공역에서의 항등변환과 같다.
역변환이 선형변환일까? 조건에 만족하려면 두 벡터의 합과 스칼라배에 닫혀 있어야 한다.
정리를 하면 T 뿐만 아니라 T의 역변환도 선형변환이다.
행렬 벡터적으로 표현할 수 있다는 뜻이다.
행렬과 행렬의 곱에서는 순서를 바꾸면 값이 달라진다.
가역행렬과 역행렬의 경우에는 순서는 중요하지 않다.
5. 역수와 행렬식 구하기
역변환 판별하는 방법 추론하기
A라는 행렬을 기약행사다리꼴 모양으로 바꿔준다. 선형 변환이다. T(x) = Sx
이렇게 바꿔준 포맷을 단위행렬에도 똑같이 행해준다. 이것이 행렬 S이다.
행렬 S 와 A를 곱해주면 기약행사다리꼴 한 모양이 나온다.
이렇게 기본행연산 과정을 계속 반복해주면 S3S2S1A 를 구하게 된다.
이것이 A의 역변환이다.
변환행렬 A를 가지고 여러번 기본행연산을 하게 되면 행렬 곱으로 나타낼 수 있다.
A에 대해 진행하는 것과 동일하게 단위행렬에 대해 진행해야 한다.
A 자리에 단위행렬을 얻게 될 때, 기약행사다리꼴을 얻게 된다.
이것이 A의 역함수로 변환된다.
S3S2S1A = I 인데, A의 역함수와 A를 곱하면 그 자체가 나오기 때문이다.
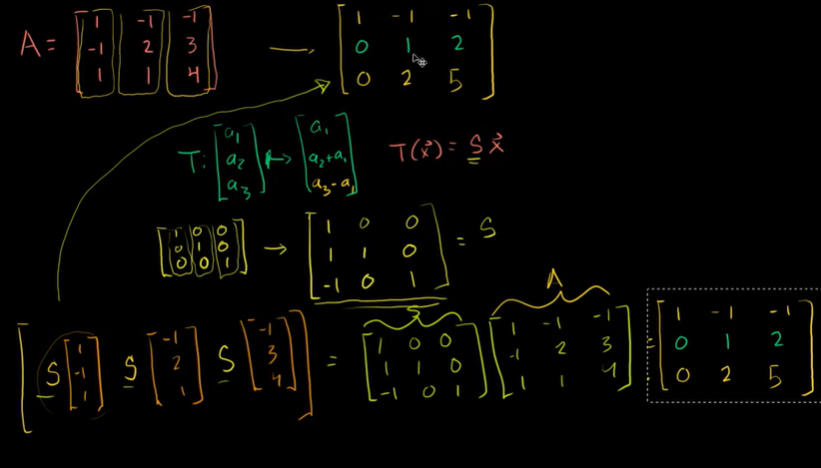
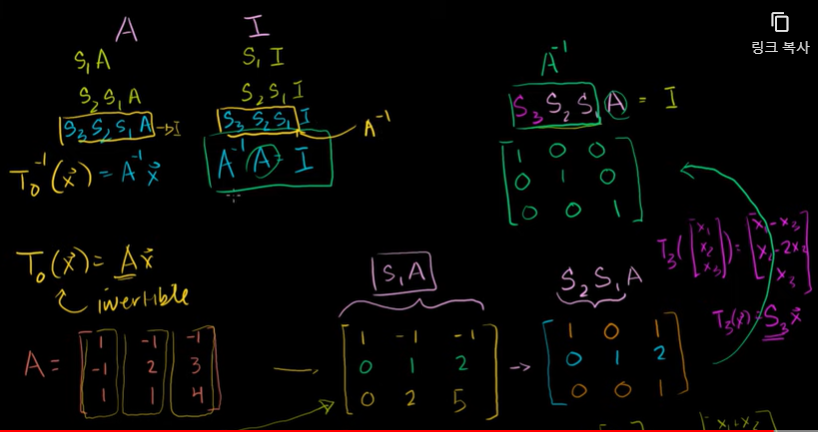

역행렬 구하기 예제
행렬 옆에 단위행렬로 된 항등행렬을 놓는다.
A를 기약행사다리꼴로 만들고, A를 항등행렬로 만드는 변환행렬은 그 자체가 항등행렬이다.
이 항등행렬이 바로 A의 역행렬이다.
즉, 좌변을 기약행사다리꼴로 만들어 항등행렬이 되면, 우변엔 역행렬이 나온다.
2 x 2 역행렬의 식
행렬식 (determinant) = Det(A) = ad - bc
행렬식이 0이 되면 역행렬은 존재하지 않는다. 1/0 이 되기 때문이다.
행렬은 괄호로 묶어 나타내고, 행렬식은 직선으로 묶어 나타낸다.
A의 역행렬은 아래와 같다.


3 x 3 행렬식
해당 행과 열을 제외한 것을 안에 집어넣는다.
한 칸 넘어갈 때마다 부호를 바꿔준다.

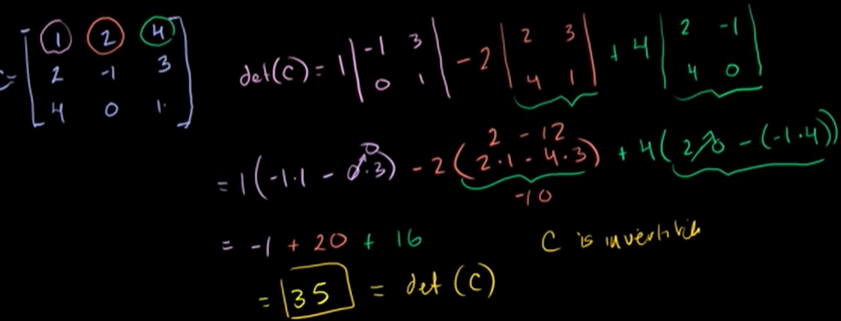
n x n 행렬식
n x n 행렬식에서 a11 의 행렬식은 (n-1)x(n-1)인데, 이 행렬식을 구하는 것은 어렵다.
하지만, 이러한 정의를 반복해가다 보면 2x2 행렬식으로 줄일 수 있다.
점화식(recursive formula)
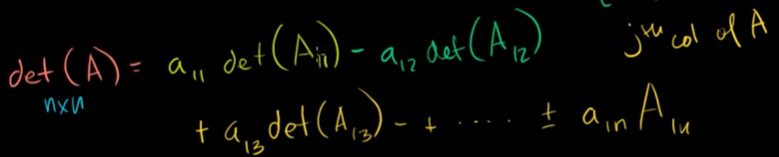


다른 행/열을 이용하여 행렬식 구하기
0이 많은 행/열을 고를 수 있다.
부호를 고를 때에는 한번씩 갈아타면 된다.
체스판 규칙을 떠올리자.
-1 ^(i+j) 로 쉽게 계산할 수도 있다.
사루스 법칙의 행렬식
빠르게 계산하는 방식이다!
3x3 행렬식이라면 두 열을 다시 적어서 3개의 곱을 구하고 3개의 곱을 빼면 된다.

6. 행렬식 심화
행을 스칼라로 곱했을 때의 행렬식
행렬 전체에 스칼라를 곱하면? 행렬식에 스칼라를 두 번 곱한 값과 같게 된다.
행렬의 한 행에만 스칼라를 곱해주어야 한다.
n x n 행렬에서도 마찬가지이다. 하나의 행에 스칼라 k를 곱해주면, 행렬식에 k 를 곱해준 값과 같다.
만약 행렬 전체를 k로 곱하면 행렬식에 k^n 을 곱해준 것과 같게 된다.
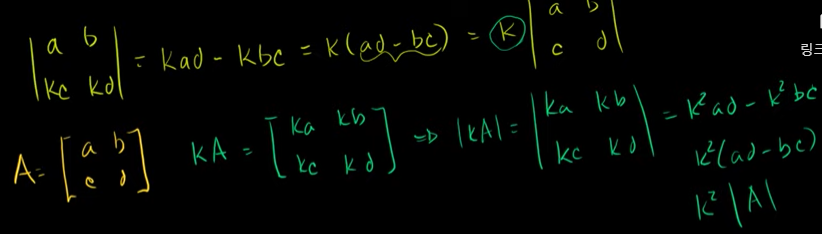
아래 시그마 수식에서 Aij 는 틀린 것이다. 겉에 작대기 두 개를 씌워주어야 한다.
부분행렬이 아닌 부분행렬의 행렬식을 곱해주는 것이 맞다.
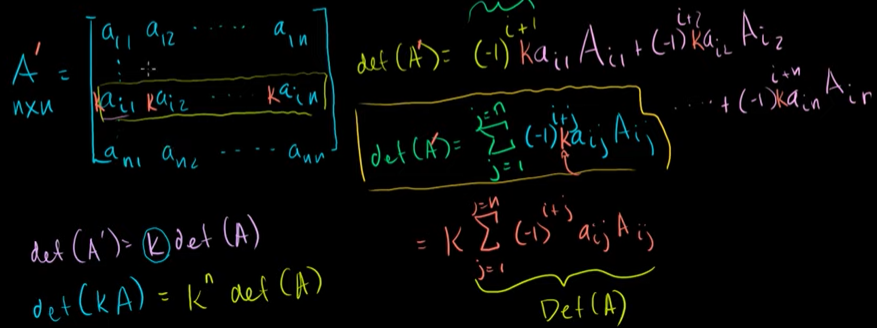
행이 더해졌을 떄의 행렬식
세 개의 행렬이 하나의 행을 제외하고 모두 동일한~
그 중 하나의 행렬의 특정한 행이 나머지 두 행렬의 특정 행의 합과 같은 특별한 경우에서!
Z의 행렬식은 X의 행렬식 + Y의 행렬식이다.
주의해야 할 것은, Z ≠ X + Y 라는 것이다.

복제된 행의 행렬식
i 와 j 를 바꾼(swap) 행렬이 있다. 교환행렬.
교환행렬의 행렬식은 원래 행렬 행렬식의 음수와 같다.
i 행과 j 행이 완전히 똑같다면 두 행을 바꾼 행렬 S는 A와 똑같다.
이 때는 det(A) = - det(A) 이므로 행렬식이 0이어야 하는 것을 알 수 있다.
같은 행이 존재하면 절대 단위행렬을 만들 수 없다. 행렬식이 0이 되면 역행렬이 절대 존재하지 않는다는 뜻이기도 하다.
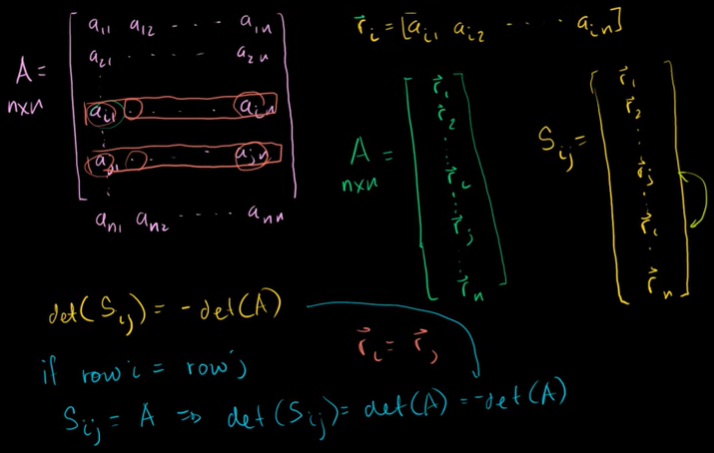
행연산 후의 행렬식
행렬에서 어떤 행을 그 행에서 다른 행의 스칼라 배수를 뺀 값으로 대체한다면 행렬식은 달라지지 않는다.
j번째 행을 j행에서 i행과 c의 곱을 뺀 값으로 대체한다면 행렬식은 바뀌지 않는다.


상삼각행렬식
주대각선 아래 0만 가지고 있을 경우, 행렬식은의 값은
주대각선 선상에 있는 것들만 곱한 값이 나온다.
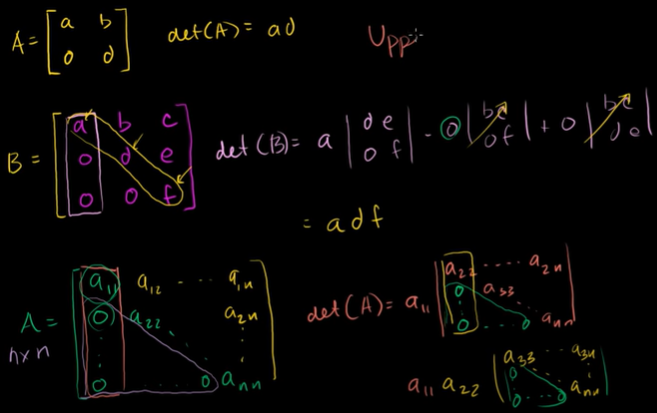
간단한 4x4 행렬식
두 가지 개념을 사용한다. '복제된 행의 행렬식'과 '상삼각행렬식'
상삼각행렬식을 만들기 위해 행을 바꿔도 된다. 바꾸면 음수로 바꿔주어야 한다.

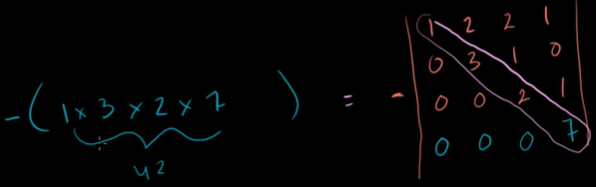
행렬식과 평행사변형의 영역
평행사변형의 넓이를 구하려면 v2의 정사영을 구하고 이것을 높이 H와 곱해주어야 한다.
정사영을 구하는 공식은 전에서 배웠다. 피타고라스의 정리를 이용해서 풀어준다.
평행사변형 A의 넓이는 행렬식det(A) = |ad-bc| 이다.
행렬식이 바로 열벡터로 이루어진 평행사변형의 넓이와 같다는 것이다.
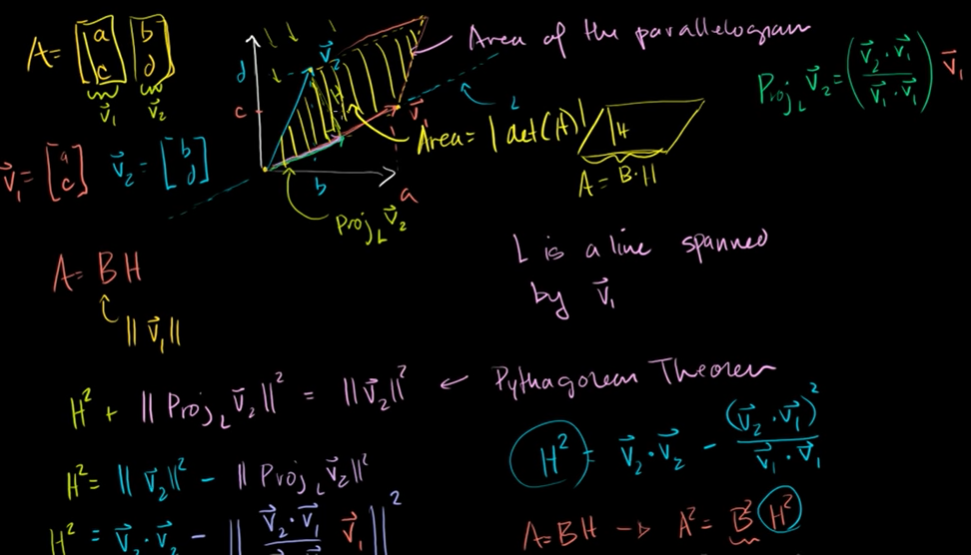

스케일 변환인자로써의 행렬식
T(rectangular) = T변환을 거친 직사각형의 상. image of rectangular under T
변환된 두 개의 벡터로 이루어진 평행사변형을 만들 수 있다.
평행사변형의 넓이는 |k1*k2*(ad-bc)| 이다.
기존 행렬식(det(A)) x 원래 직사각형의 넓이(k1*k2) 와 같다.
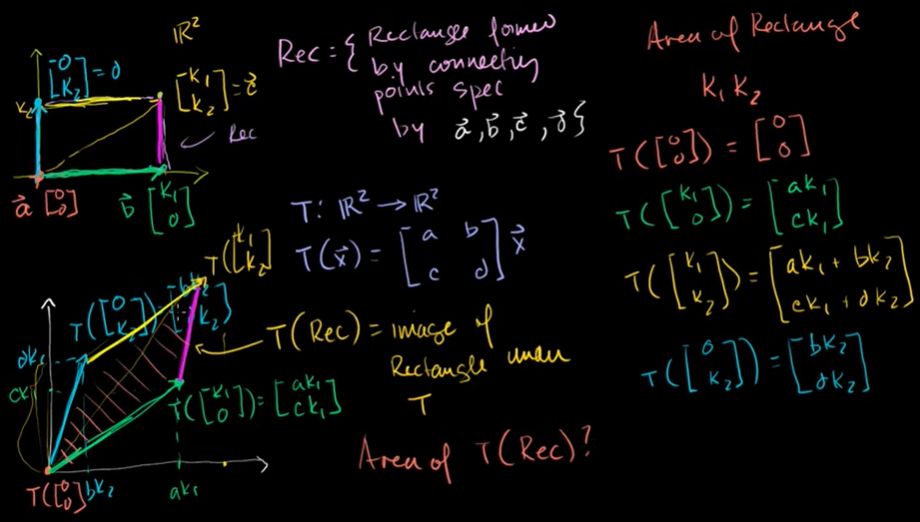
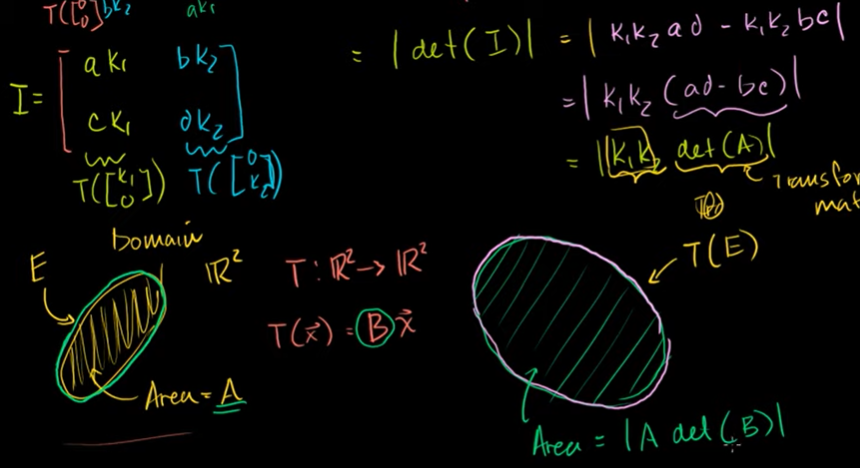
새로운 타원의 넓이 = 기존 넓이 x 변환에 쓰인 행렬의 행렬식
7. 전치행렬
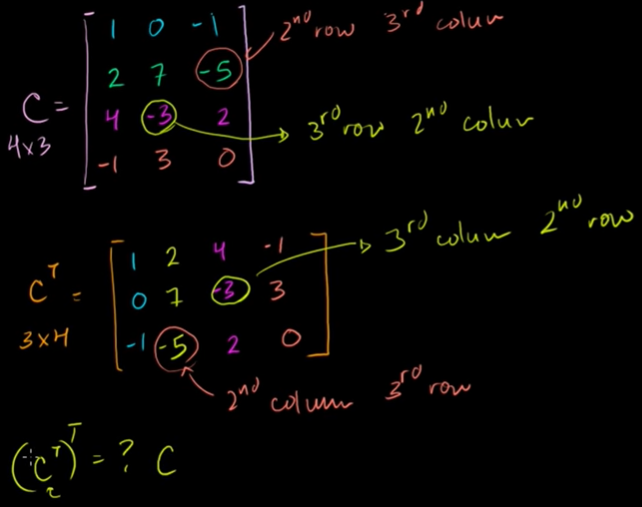
전치행렬
모든 행과 열이 바뀐 행렬이다.
2nd row, 3rd column → 3nd row, 2nd column
전치행렬을 전치하면 제자리로 돌아온다.
전치행렬의 행렬식
전치행렬의 행렬식은 기존 nxn 행렬의 행렬식과 같다.

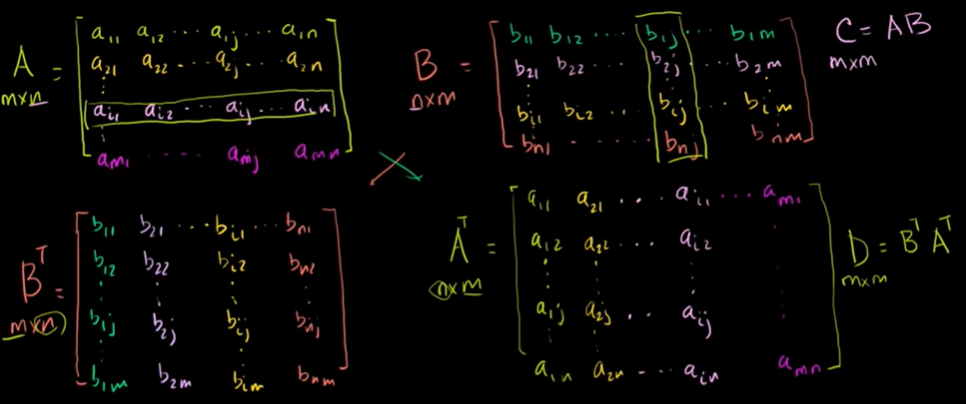
행렬곱의 전치행렬
행렬곱 C의 i번째 행, j번째 열에 있는 것 = 행렬곱 D의 j번째 행, i번째 열에 있는 것
행렬의 곱의 전치행렬 = 행렬 각각을 전치시킨 후 순서를 바꿔 곱한 행렬
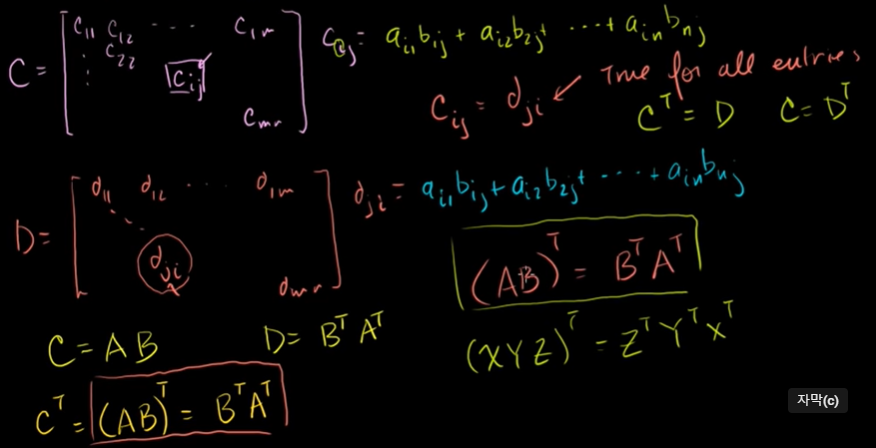
전치행렬의 합과 역
합한 행렬에서의 원소는 각각 행렬의 원소의 합이다.
A와 B를 더해 C가 된 행렬을 전치해줄 때,
C 전치행렬의 원소 = A 전치행렬의 원소 + B 전치행렬의 원소
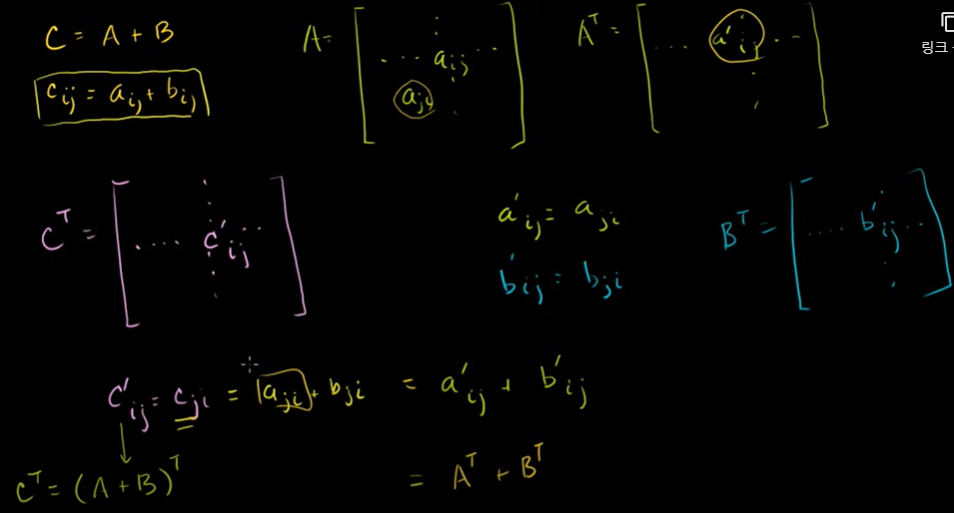
단위행렬의 전치행렬은 대각선이 그대로이기 때문에 단위행렬 그 자체이다.
A의 역행렬의 전치행렬 = A 전치행렬의 역수
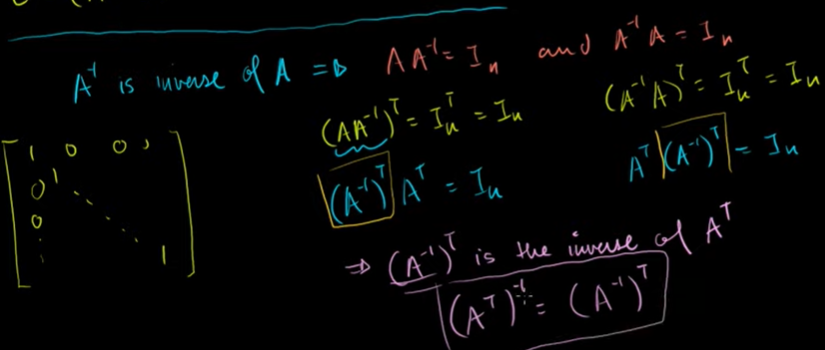
전치벡터
벡터를 전치한 것은 열벡터를 행벡터로 바꾸는 것이다.
벡터 v 와 w 를 내적 = v의 전치행렬 x w
행렬과 행렬의 곱 = 각각의 행과 열의 내적
또 하나의 공식 (Ax) · y = x · (A^T * y)

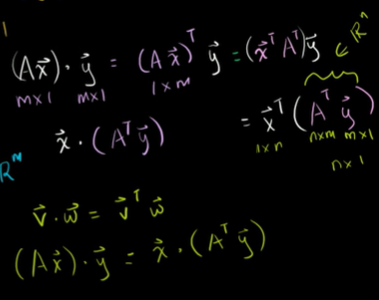
행공간과 좌영공간
영공간을 구할 때, 행렬이 영벡터가 되도록 기역행사다리꼴 형태로 만들어준다.
여기서 나오는 피벗변수를 이용해서 식을 만들어준다.
이 식에서 나오는 벡터가 영공간의 선형결합이 된다. span 으로 묶을 수 있는 것이다
열공간은 행렬 안에 있는 벡터들의 선형결합이 만든 부분공간과 같다.
열벡터들의 생성이다.
여기서 선형독립인 기저를 찾을 수 있다. 기저가 하나라면 Rank(A) = 1이다.
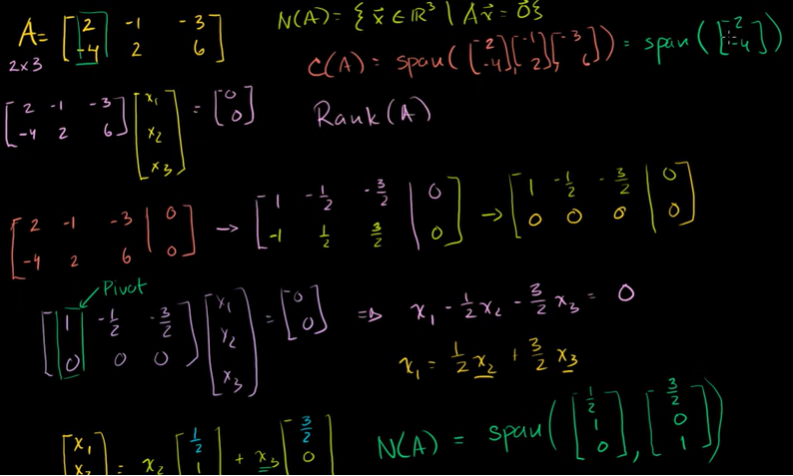
전치행렬로 만들어서 계산할 때도 마찬가지이다.
영공간을 찾을 때에는 기약행사다리꼴로 만들어주고 피봇변수를 찾아서 새롭게 정의해야 한다.
그리고 선형결합을 이용한 생성을 만들 수 있다.
열공간은 피봇열만 생각해주면 된다.
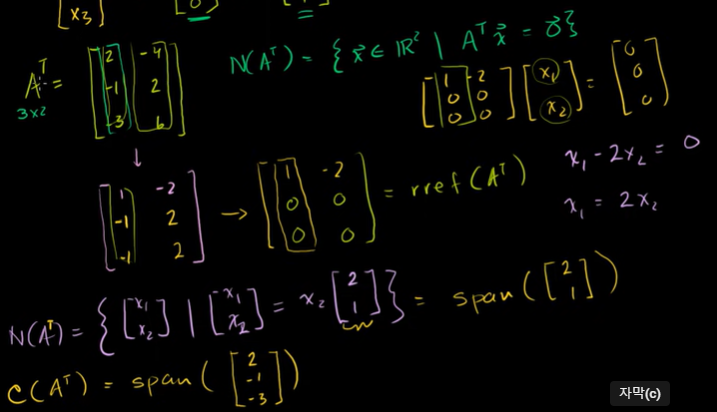
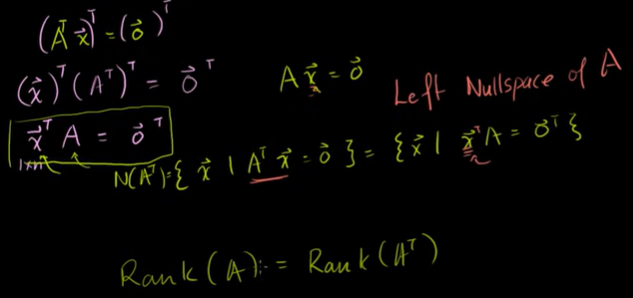
전치행렬의 열생성은 A의 행 공간이다.
전치행렬의 영공간을 구할 때
전치행렬과 벡터를 곱한 것이 영벡터가 되는 모든 부분집합을 찾는다.
이와 똑같이 계산을 할 수 있는 것이 좌영공간이다.
좌영공간(left nullspace of A)은 x 가 왼쪽에 있다.
좌영공간은 전치의 영공간
A의 좌영공간은 R^2의 직선이다.
A의 행공간은 R^3의 직선이다.
A의 열공간은 R^2의 직선이다.
A의 계수 = 전치행렬 A의 계수
전치행렬에서 몇 개의 열이 선형독립하는지는 원래 행렬에서 몇 개의 행이 선형독립하는지와 같다.
좌영공간과 행공간의 시각화
C(A), N(A^T)
열벡터와 좌영공간(전치의 영공간)의 임의의 벡터는 직교한다.
둘을 내적하면 0이 된다.
A의 열공간이 A의 전치의 영공간과 직교한다. →
A의 열공간이 A의 좌영공간과 직교한다 (= A의 전치의 행공간은 A의 전치의 영공간과 직교한다.)
N(A), C(A^T)
A의 영공간은 R^3에 존재하는 벡터의 생성이다. 벡터의 임의의 선형결합이다. 평면이라고 할 수 있다.
A의 행공간은 A의 전치의 열공간이라고 할 수 있다.
행공간의 임의의 원소를 영공간의 임의의 원소와 내적하면 0이 나온다. 직교한다는 뜻이다.
A의 영공간이 A의 전치의 열공간과 직교한다 →
A의 행공간이 A의 영공간과 직교한다. (= A의 전치의 열공간이 A의 전치의 좌영공간과 직교한다.)
A의 좌영공간이 A의 전치의 영공간 인 것처럼,
A의 영공간은 A의 전치의 좌영공간이다.
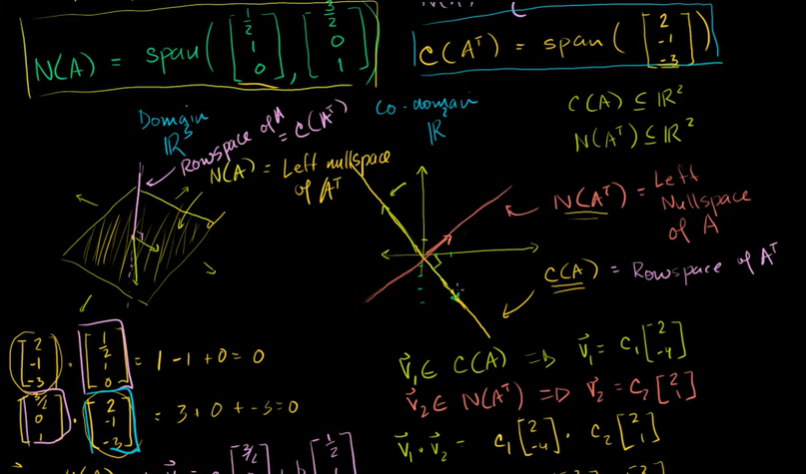
rank(A) = rank(A의 전치행렬)
rank(A의 전치행렬) = 열공간의 차원 dim(C(A^T))
A 전치의 열공간은 A의 행공간이다.
기저를 구하고 싶다면, 열을 구성하는 선형독립벡터의 최소한의 집합을 구해야 한다.
A를 기약행사다리꼴로 만들자.
행공간을 위한 기저가 필요하다. 피벗행들의 선형결합으로 나타낼 수 있다면 선형독립하며 유효한 기저가 된다.
기약행사다리꼴의 피벗행들은 A의 행공간을 위한 기저가 된다.
즉, A의 전치의 열공간을 위한 기저가 된다.
A의 피벗행의 개수를 세면 된다. 혹은 피벗성분의 개수를 세면 된다.
'A의 전치행렬 x A'의 가역성 확인하기
역행렬은 영공간이 영벡터만 가지는 것이다.
정방행렬을 만들기 위해 A의 전치행렬과 A의 곱을 만들어준다.
열들이 선형독립인 정방행렬(k x k)이 있다면, 추축열이 k개이다.
여기서 단위행렬을 찾았다면 역행렬이 존재한다는 것이다.
A의 열들이 선형독립이라면 A 전치행렬과 A의 곱의 열들은 선형독립이다. 역행렬이 존재한다.
양변에 전치행렬을 곱해준다.
벡터와 행렬을 곱해주면 결국에는 벡터가 나온다.
벡터의 전치행렬과 벡터를 곱하는 것은, 그 자신을 내적한 것과 같다.
v는 전치행렬의 영공간의 원소이다. v는 영벡터일 수밖에 없다.
A의 전치행렬과 A의 곱이 영공간이라는 것은 유일한 해가 영벡터라는 뜻이다.
선형독립이라는 뜻이다. 그리고 정방행렬이기에 단위행렬이 있어서 역행렬이 존재한다는 것을 증명한다.
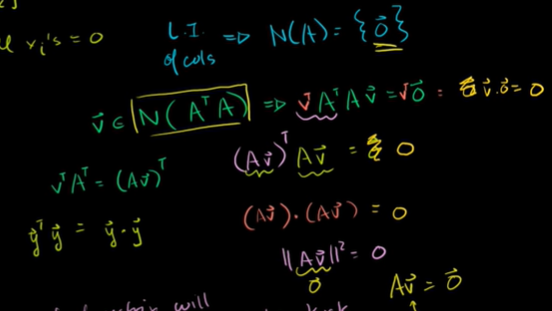
'Mathematics and Statistics' 카테고리의 다른 글
| Review >> Essence of Linear Algebra_3Blue1Brown (1) | 2024.01.14 |
|---|---|
| Essence of Linear Algebra_3Blue1Brown (2) | 2024.01.14 |
| Review >> Linear Algebra_Khan (2) | 2024.01.09 |
| Linear Algebra_Khan [3/3] 상호 좌표계(기저) (1) | 2024.01.09 |
| Linear Algebra_Khan [1/3] 벡터와 공간 (1) | 2023.12.28 |
