understanding matrix and vector operations through that more visual lens of linear transformations
Ch1. Vectors
벡터에 대한 3가지 관점
물리학 학생의 관점에서 벡터는 공간에서 화살표. 크기와 방향이다.
컴퓨터 과학 관점에서 벡터는 순차 숫자 리스트.
수학자 관점에서 벡터의 연산이다. vector addition & scalar multiplication
Ch2. Linear Combinations, span, and basis vectors
좌표계를 기저벡터로 표현할 수 있다.
스칼라와 기저벡터 조합으로 모든 공간을 표현할 수 있다.
이것을 선형 결합 (linear combination) 이라고 한다.
set of all possible vectors that you can reach with a linear combination of a given vectors
is called the 'span' of those two vectors
- the span of these vectors is the set of all possible linear combinations.
선형 종속이면 다른 벡터의 선형 결합으로 해당 벡터를 그릴 수 있다.
각 벡터가 생성에서 다른 차원을 추가한다면 선형독립이다.
Ch3. Linear transformatoins and matrices
선형 변환은 사실 함수(function)이다. 벡터가 들어가서 벡터가 나오는 것이다.
선형 변환이라면 격자 라인들이 변형 이후에도 여전히 "평행"하고 "동일한 간격"으로 있어야 한다. 원점에 고정되어야 한다.(fix the origin in place)
선형변환에서 행렬의 열을 기저벡터의 변환된 형태로 기억하는 것이 좋다.
(transformed versions of your basis vectors)
그 결과는 변환된 벡터들의 선형조합으로 여기는 것이 재밌다.
(think about the results as the appropriate linear combination of those vectors)
선형변환을 할 때는 공간에서 단위벡터가 어떻게 돌아가는지를 먼저 행렬로 확인해놓은 후에, 특정 벡터를 곱해 어디로 가는지를 확인하면 된다.
i-hat 과 j-hat 벡터가 선형종속(linearly dependent)이라면 벡터 하나가 다른 벡터의 스케일링 버전이다. 이 선형 변환은 2차원 공간을 수축(squish)시켜 두 벡터가 놓여있는 1차원 공간인 선으로 만든다. 선형 종속인 두 벡터의 스팬(span)이다.
선형변환은 공간을 이동시키는 방법이며, 격자선이 여전히 평행하고 균등간격을 유지한 변형이다.
(move around the space) (Grid lines remain parallel and evenly spaced)
변환된 행렬의 열들은 단위벡터의 좌표값을 나타내며, 행렬-벡터 곱은 단지 이것을 계산하는 방법이다.
(where i-hat lands, where j-hat lands)
행렬을 볼 때마다 공간의 어떤 변환으로 생각하면 쉽다 (certain transformation of space)
Ch4. Matrix multiplication as composition
두 행렬의 곱셈은 기하학적으로 한 변환을 적용하고나서 다른 변환을 적용한 것과 같다
함수를 합성할 때 오른쪽에서 왼쪽으로 읽어야 한다.
행렬곱을 암기식이 아닌 이해를 위해 접근해보자.
왼쪽 행렬을 오른쪽 행렬의 첫 번째 열로 곱하면 공간을 변환한 것으로 이해할 수 있다.
e g 벡터를 a b c d 행렬에 곱한 것은 e 를 a c 벡터에 곱한 것이고, g를 b d 벡터에 곱한 것이다.
각각 합치면 벡터가 행렬에 맞춰 어떻게 변화하는지를 볼 수 있는 것이다.

교환법칙 AB ≠ BA
- 기하학적으로 변환하는 순서가 달라지기 때문에 결과값도 달라진다.
결합법칙 (AB)C = A(BC)
- 기하학적으로 오른쪽 끝에서 왼쪽으로 변환을 적용하는 것은 달라지는 것이 없기 때문에 결과값도 동일하다.
Ch5. 3-dimensional linear transformations
3D 행렬곱은 컴퓨터그래픽이나 로보틱스에서 유용하다.
Ch6. Determinant
Exactly how much are things being stretched or squished?
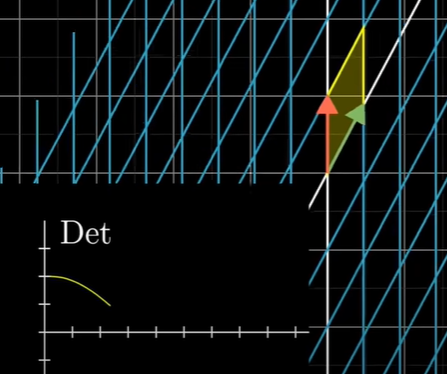
선형변환에 의한 영역의 변화를 나타내는 팩터가 행렬식(determinant)이다.
행렬식의 값이 2이면 영역의 넓이도 2배 커지는 것이다.
-2 같은 음수라면 영역이 어떻게 되는 것일까? 종이를 뒤집는 것과 같다. 공간이 뒤집히고 2배 커지는 것이다.
i-hat 이 j-hat 가까이로 갈수록 행렬식(determinant)은 줄어든다.
완전히 한 선을 이루면 행렬식은 0이다. 계속해서 넘어가면 행렬식은 음수가 될 수 있다.
3차원에서는, 부피(volume)가 스케일링되는 것을 보여준다. 평행6면체의 부피이다.
행렬식 값이 0이라면 모든 공간이 찌부려져서 평면이나 선, 점까지 될 수 있다.
방향이 전환되어서 오른손 법칙이 아닌 왼손 법칙이 적용된다면 행렬식 값은 음수가 된다.
행렬식의 공식은 ad-bc 이다. 왜일까?
b와 c의 값을 0으로 만들 때, 행렬식은 ad이다.
a는 i-hat이 얼마나 뻗어있는지를 말해주고, d는 j-hat이 얼마나 증가했는지를 말해준다.
ad는 직사각형의 넓이이다.

b의 값이 존재하더라도 평행사변형이기 때문에 넓이는 ad 이다.
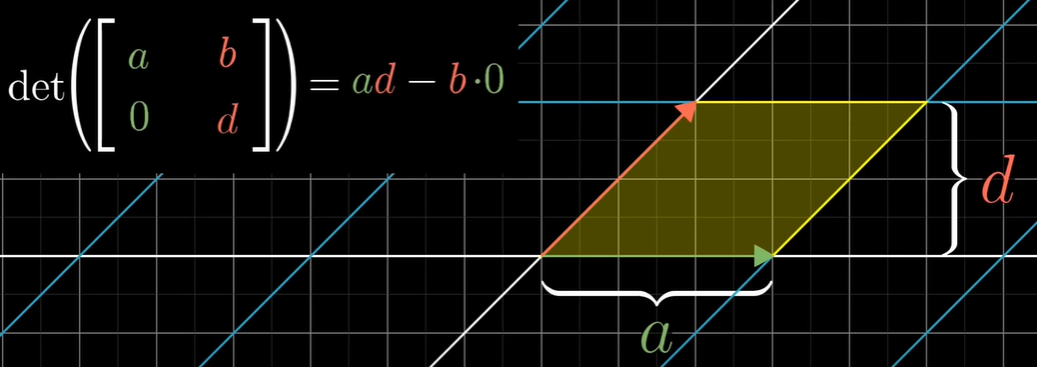
b, c가 둘 다 0이 아니면 bc는 평행사변형이 얼마나 대각선 방향으로 늘려지고 찌그러지는지를 알려준다.

Ch7. Inverse matrices, columns space and null space
선형대수학의 유용성은 어떤 방정식계이든지 해결할 수 있다.
각 방정식 내에서 각 변수들의 역할은 어떤 상수를 스케일링하는 것이다.
이것이 선형 방정식계이다.

행렬 A는 선형변환을 나타낸다.
x를 찾는 것은 어떤 벡터가 선형변환을 거쳐 v가 나오는 것인지 찾는 것이다.
Inverse matrices (역행렬)
x를 찾기 위해서 v에서 A 행렬의 역재생을 하면 찾을 수 있다.
A^-1 A 아무것도 일어나지 않는 변환을 "항등 변환(identity transformation)"이라고 부른다.
만약 역행렬이 평면이나 선, 점으로 축소시킨다면 행렬식은 0이다.
Column space (열공간)
행렬의 가능한 결과의 집합 (set of all possibgle outputs of Av)
열공간이라는 이름은 행렬의 열이 기저벡터의 변환 후 위치이기 때문이다.
변환 후 기저벡터들의 확장공간은 가능한 모든 결과공간을 알려준다.
열공간에는 항상 영벡터가 존재하는데, 선형변환은 반드시 원점이 고정되어 있어야 하기 때문이다.
Rank (차원)
그래서 rank의 보다 정밀한 정의는 열공간의 차원 수 이다.
Null space (영공간)
원점으로 이동되는 벡터들의 집합. 영벡터로 이동하는 모든 벡터들이다.
kernel 이라고도 불린다.
선형 방정식계 용어로 말하면, 벡터 v가 영벡터의 경우, 영공간 모두가 해가 될 수 있다.
Ch8. Nonsquare matrices as trnasformations between dimensions
3 x 2 행렬
2개의 열은 입력공간의 두 기저벡터를 말한다.
3개의 행은 기저벡터의 도착지로 3개의 다른 좌표값을 나타낸다.
2차원 공간을 3차원 공간으로 변환한 것이다.
2 x 3 행렬
3개의 열은 3개의 기저벡터를 가진 입력공간에서 시작했다는 뜻. 3차원에서 시작했다는 뜻
2개의 행은 세 기저벡터의 변환후에 좌표값 2개를 가지고 있다는 뜻. 2차원으로 이동해야 한다.
3차원에서 2차원으로 변환된 것이다.
Ch9. Dot products and duality
Dot products (내적)
내적을 구하는 것은 같은 좌표값으로 짝을 지어 곱한 후 더하는 것이다.
w 벡터가 v 벡터 선 위로 투영된 이 길이에 벡터 v의 길이를 곱하는 것이다.
w 벡터의 정사영이 v와 반대 방향이라면 내적의 결과는 음수가 된다.
벡터가 비슷한 방향이면 내적값이 양수이고, 수직이면 내적의 결과가 0이다.
v와 w의 순서는 중요하지 않다. v가 w위로 정사영된 것을 생각해도 동일하다.

v를 2배 스칼라배하더라도 w가 v위에 정사영되는 길이는 동일하기 때문에 내적의 결과는 동일하다
v가 w위에 정사영되는 길이는 정확히 2배가 되기 때문에 동일하다.

Duality (이중성)
내적과 정사영은 무슨 상관일까?
1 x 2 행렬과 2차원 벡터 사이에는 관련성이 있다.
벡터의 숫자 표현을 옆으로 기울여서 연관 행렬을 얻을 수 있다.
벡터를 숫자로 바꿔주는 선형변환과 벡터 그 자신과의 관계이다.
2차원 공간을 1차원 선으로 변환했을 때
i-hat을 u 벡터 위에 정사영한 것과 u-hat을 x축에 정사영 한 것의 길이는 같다.
이것은 u-hat의 x축 좌표와 같다.
j-hat을 u 벡터 위에 정사영한 것은 u-hat의 y축 좌표와 같다.
결국, i-hat과 j-hat을 정사영한 것이 u-hat의 x,y축 좌표이다.
이 좌표로 1x2 행렬을 만들 수 있다.


투영 변환을 나타내는 1x2 행렬은 u-hat의 좌표가 된다.
임의 벡터[x y]의 투영은 이 행렬에 임의벡터를 곱하는 것이다.
이것은 계산적으로 u-hat과의 내적과 똑같다.
단위벡터와의 내적과 벡터를 단위벡터로 투영한 길이를 구하는 것이 같다. 이것이 이중성(duality)이다.

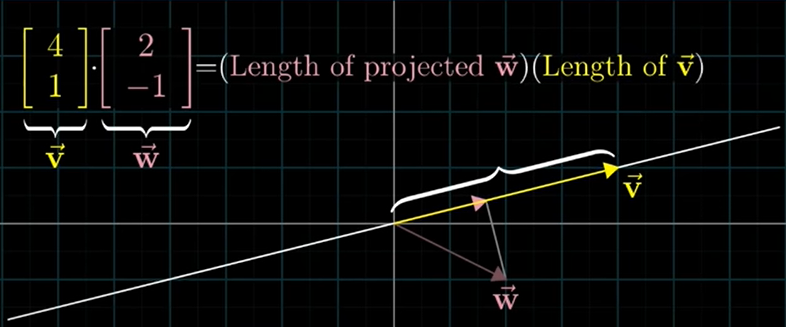
Nonunit vectors
비단위벡터의 내적은 벡터 위로 투영한 후, 벡터의 길이만큼 투사체 길이를 늘리는 것이다.
때로는 공간 속의 화살표보다 선형변환의 물리적 실체로 이해하는 편이 더 쉬울 때가 있을 것이다.

Ch10. Cross products
외적은 평행사변형(parallelogram)의 넓이이다.
v가 w의 오른쪽에 있으면 외적값은 양수이고, 왼쪽에 있으면 단위벡터의 방향이 바뀌었으니까 음수이다.
이것은 순서가 중요하다는 의미이다. v와 w를 뒤집으면 그 값의 마이너스가 된다.

v와 w벡터로 이루어진 행렬은 i-hat 과 j-hat을 v와 w 로 선형 변환하는 것이다.
행렬식은 이 변환으로 어떻게 공간이 변화하는지를 측정하는 것이다.
i-hat과 j-hat으로 이루어진 1길이의 정사각형이 선형변환을 거치며 평행사변형(parallelogram)이 된다.
두 개의 벡터가 수직이면(perpendicular) 평행사변형의 넓이는 보다 클 것이다.
두 개의 벡터가 나란히 있다면 그 넓이는 보다 작을 것이다.
만약, 하나의 벡터가 3배 스칼라배 되었다면 공간도 3배 커진다.



진정한 의미의 외적은 두 개의 3D 벡터를 결합해 새로운 3D 벡터를 구하는 것이다.
외적의 결과는 숫자가 아니라 벡터이다.
평행사변형의 면적이 이 새 벡터의 길이와 같다.
그래서 새 벡터의 방향은 평행사변형에 수직한 방향이다.
어느 방향으로 수직한지는 오른손 법칙을 사용하면 된다.
외적의 공식은 다음과 같다.
행렬식을 이용해서도 도출할 수 있는데 기저벡터를 왼쪽 열에 넣어서 만든 선형 조합으로 표현된 벡터는 v와 w벡터에 수직한 유일한 벡터가 된다.
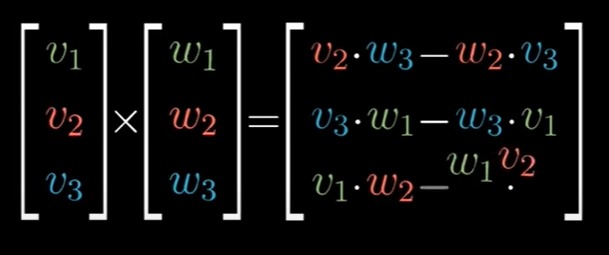
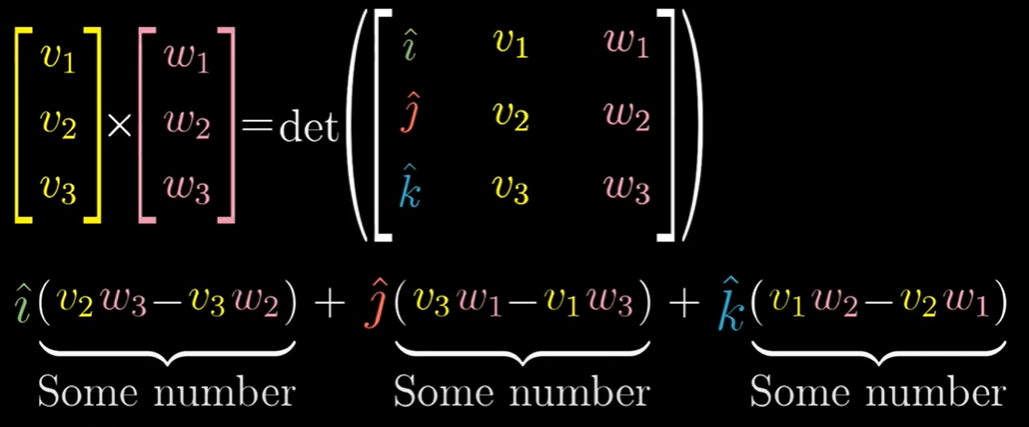
Ch11. Cross products in the light of linear transformations
어떤 공간을 number line으로 선형변환을 할 때마다 그 공간의 한 특정 벡터와 연관이 있다.
선형변환을 하는 것이 특정 벡터의 내적을 구하는 것과 같다.
각 열은 기저벡터가 변환된 숫자를 알려준다.
3차원에서 1차원으로의 선형변환을 정의하면, 벡터 v와 w로 정의된다.
그 변환을 3차원에서의 이중 벡터(dual vector)로 연결시키면 이것은 v와 w의 외적이 될 것이다.
이것이 외적의 기하학적 의미와 계산 사이의 관계를 명확하게 만들 것이다.
실제 3차원 외적은 두 벡터를 취해 하나의 벡터를 생성한다. 할 수 있는 방법이 있다.
3차원에서 1차원으로 가는 함수를 통해 선형변환하는 것이다. 이것은 이중성 논리에 따라 세로로 돌려 내적으로 해석할 수 있다.

p와 어떤 벡터 [x,y,z] 사이의 내적을 취하면 xyz를 행렬의 첫 번째 열에 놓고 다른 두 열에 벡터 v와 w의 좌표를 놓은 후 행렬식을 계산하는 것과 같은 결과를 갖는다.
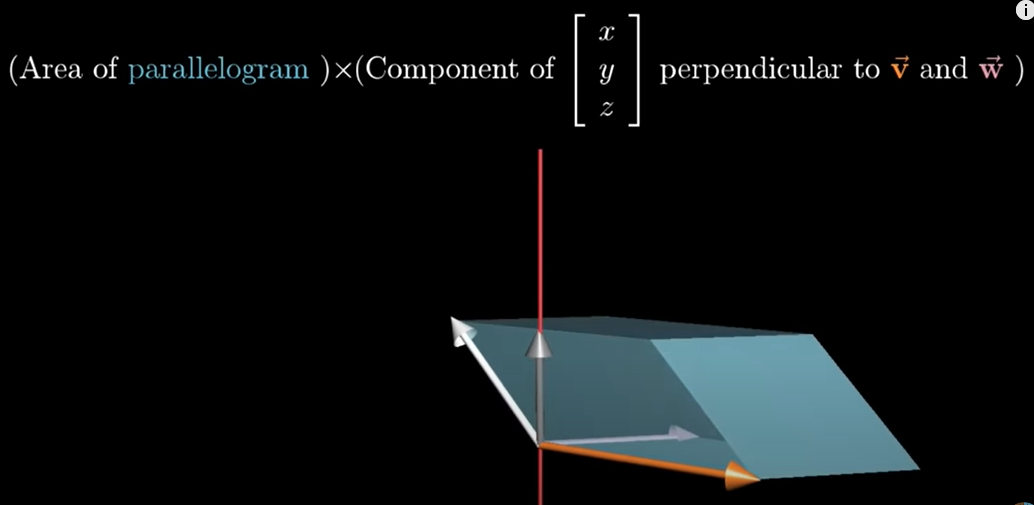
모든 입력벡터 [x,y,z]에 대해 벡터 v와 w에 의해 정의된 평행 육면체가 나온다.
v와 w 좌표의 특별한 조합들 그 상수들은 p의 좌표가 된다.


1. 벡터 p와 어떤 벡터 [x,y,z]를 내적한 것
2. [x,y,z]를 행렬의 첫 번째 열에 두고 벡터 v, w의 좌표를 다른 두 열에 놓은 후 행렬식을 구한 결과
어떤 벡터 p가 다음과 같은 속성을 가지는지를 찾는 것이다.
1. 벡터 p와 어떤 벡터 사이의 내적에 대한 기하학적 해석은 다른 벡터를 p에 투사한 후에 그 투사된 길이를 p의 길이에 곱하는 것이다.
2. 평행육면체의 부피를 구하는 방법은 v와 w벡터로 이루어진 평행사변형의 면적을 구한 후에
[x, y, z]의 길이만큼 곱하는 것이 아니라 그 평행사변형에 수직인 길이만큼만 곱한다.
이것은 [x,y,z] 그리고 v, w에 수직이면서 길이는 평행사변형의 면적인 벡터 간의 내적을 구하는 것과 같다.
이 내적이 앞에서 말한 내적과 같은 것이다.
이를 통해 기하학적 해석과 외적의 계산이 관련되어 있음을 나타낸다.


결론적으로, 외적을 계산하는 2가지 방법
i j k hat을 넣어서 행렬식을 계산하는 방법
기하학적으로는, 이중 벡터가 수직이기에 길이는 평행사변형의 면적과 같음을 이용하는 것이다.
Ch12. Cramer's rule, explained geometrically
대부분의 선형 변환의 경우 변환 전후의 내적은 매우 다르다.
내적을 보존하는 변환은 '직교정규변환'(orthonormal transformation)이라고 한다.
벡터를 단위 길이로 서로 수직으로 유지하는 것이다. 회전 행렬이라고 생각한다.
계산이 어렵지 않다.


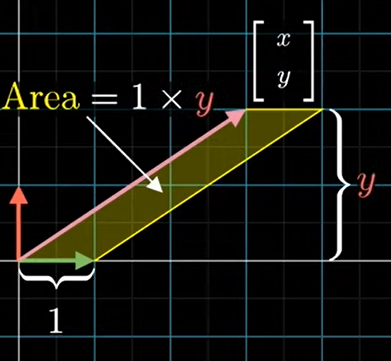
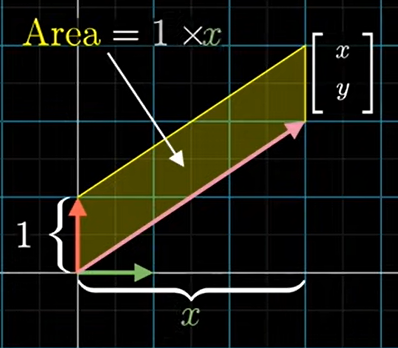
크래머 공식
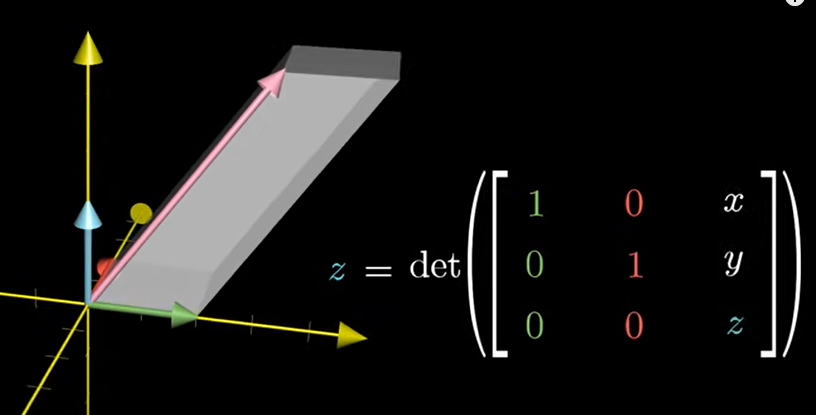
3차원에서는 벡터의 좌표 중 하나를 생각하는 방식은
z좌표라면 다른 두 개의 x,y 기본 벡터를 i-hat 과 j-hat에 걸쳐 있는 면적 1의 정사각형을 밑면으로 생각하면
그 부피는 벡터의 세 번째 좌표인 높이와 같다.


Ch13. Change of basis
다른 좌표계 사이를 어떻게 해석해야 할까?
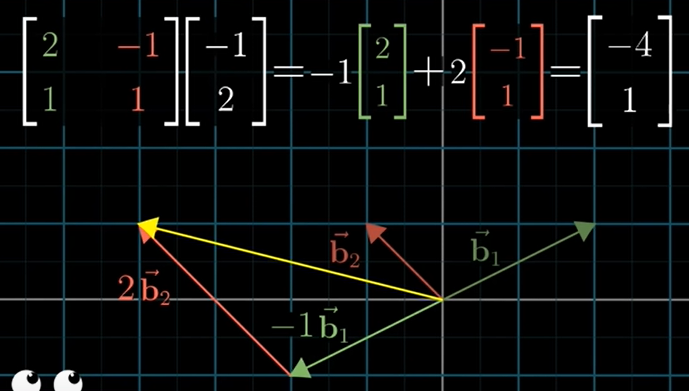
행렬벡터곱으로 표현할 수 있다.
행렬의 열은 Jennifer의 기저벡터를 표준좌표계로 나타낸다.
이것은 i-hat과 j-hat을 벡터로 곱해줘서 나타내는 것과 같다.
Jennifer의 기저벡터를 나타내는 열로 이루어진 행렬은 우리의 좌표계로 적혀 있다.
이것은 그녀의 언어를 우리의 언어로 바꿔준다.
역행렬은 그 반대를 한다.
좌표계에서 나타낼 수 있는 것이 벡터만 있는 것은 아니다.
i 와 j hat 을 반시계방향으로 90도 돌려서 우리 좌표계에 나타내는 것은 쉽다.
제니퍼의 좌표계로 돌린 것을 나타내는 것은 우리 것을 변환한다고 해결되지 않는다.
제니퍼가 원하는 것은 i와 j hat이 어디로 가는지가 아닌 그녀의 기저벡터가 어디로 가는지를 보는 것이다.
먼저 그녀의 벡터를 우리의 언어로 바꾼다.
그녀의 기저벡터를 우리의 언어로 바꾸는 열이 있는 행렬을 사용하면 된다.
그리고 나서 변환행렬을 왼쪽에 곱한다.
이것은 벡터가 어디로 움직일지를 알려준다.
대신 우리의 언어로 알려주는 것이다.
마지막으로 기저행렬의 역행렬을 왼쪽에 곱해줘서 변환된 벡터를 제니퍼의 언어로 얻을 수 있다.
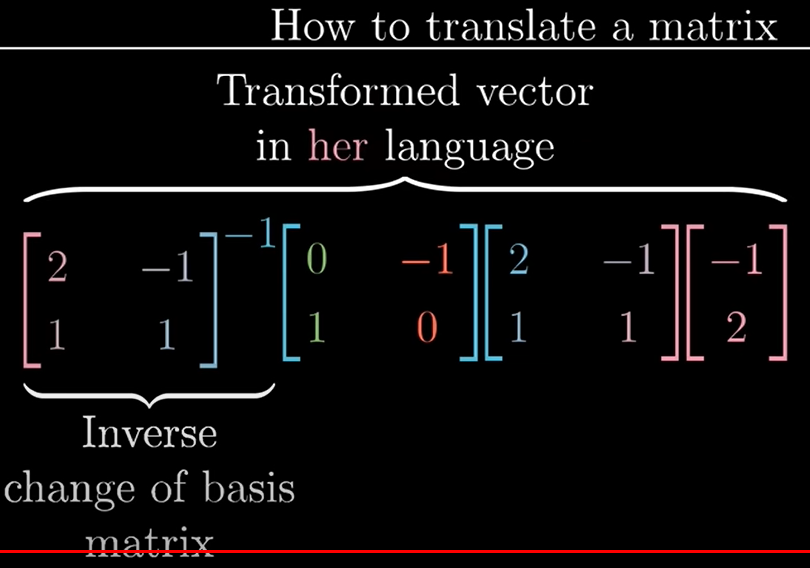
이 행렬을 그녀의 좌표계에 있는 벡터에 곱할 때 반시게 90도 변환된 버전을 그녀의 좌표계로 표현한다.
A^-1 M A v
Ch14. Eigenvectors and eigenvalues
벡터의 끝과 원점을 지난 벡터의 스팬을 생각할 수 있다.
여기서 선형변환을 하면 보통은 이 스팬에서 벗어나게 될 것이다.
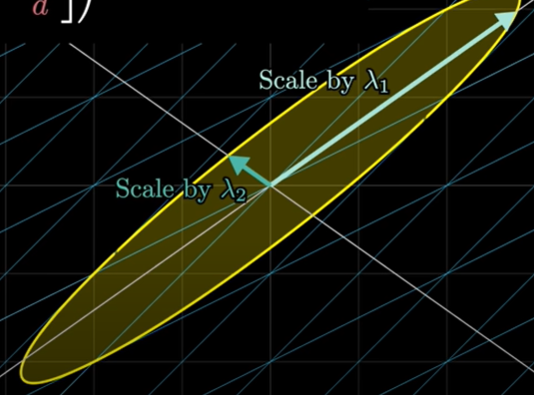
그러나 어떤 특별한 벡터는 선형변환 후에도 그 자신의 스팬에 존재할 것이다.
이것은 단지 늘어나거나 줄어든 것이다. (stretch or squish) 스칼라배된 것이다.

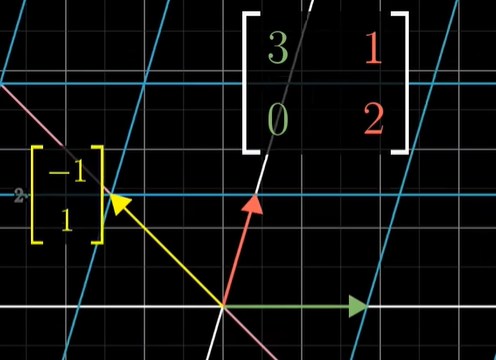
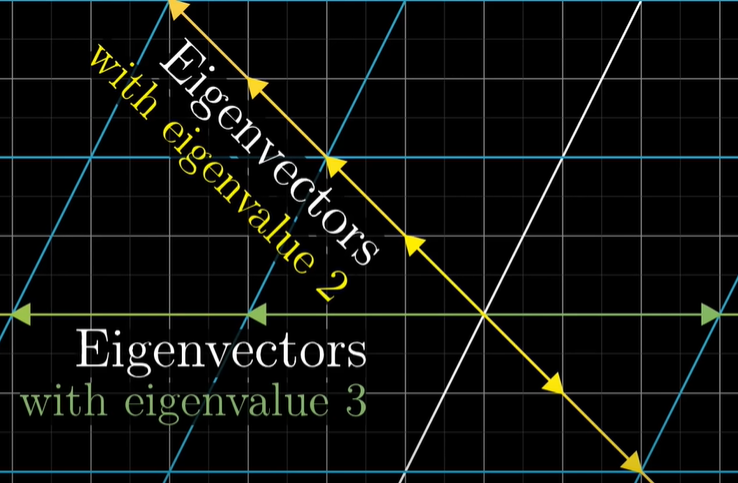
위 예시에서는 i-hat 이 위 행렬로 선형변환되어도 그 스팬에 여전히 존재하고 3배로 증가한다.
[-1 1] 벡터도 그 스팬에 여전히 존재한다. 이것은 2배로 증가한다. stretch by 2
이 특별한 벡터들이 '고유벡터' (eigenvector) 이다.
각각의 고유벡터는 '고유치' (eigenvalue) 를 가지게 된다. 변환 도중 늘어나고 줄어드는 정도의 배수이다.

3차원에서의 회전을 생각해보자.
공간에서 고유벡터를 찾으면 이것은 회전의 축을 찾은 것과 같다.
3차원 회전을 생각할 때는 3x3 행렬 전체를 생각하는 것보다 회전축을 생각하는 것이 훨씬 쉽다.
선형변환 중 일어나는 일에 대해 더 잘 이해하려면 특정 좌표계에 덜 관계있는 고유벡터와 고유값을 찾아야 한다.
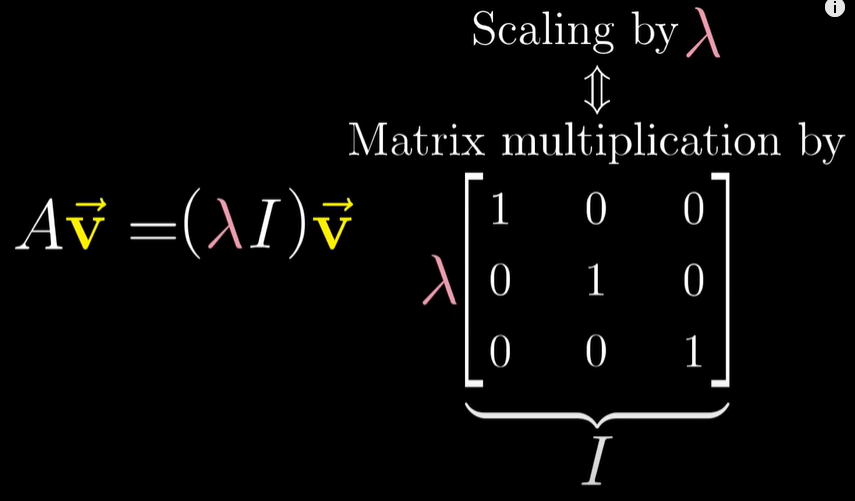
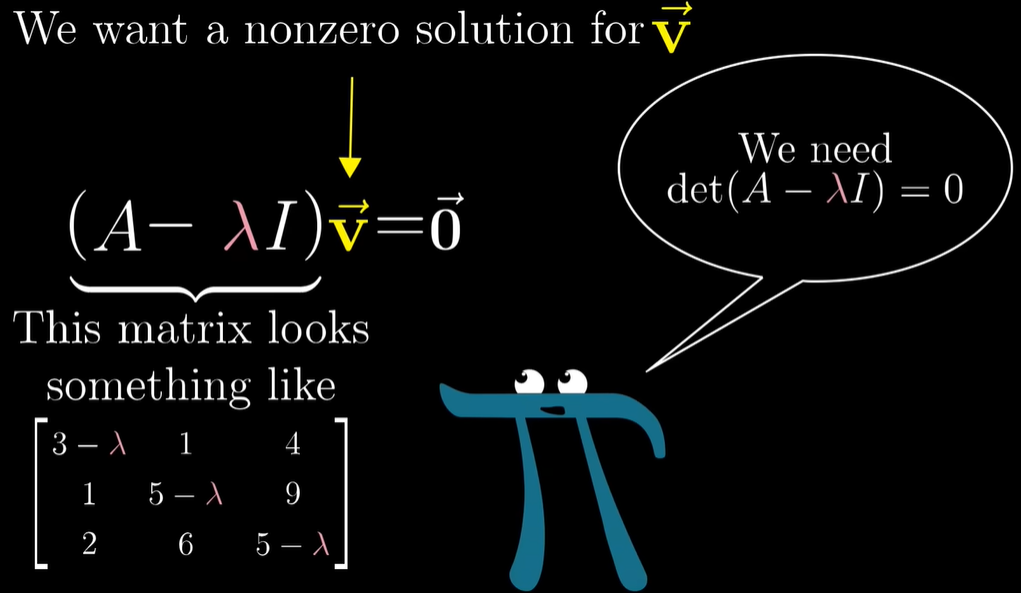
행렬벡터곱 Av 는 고유벡터를 람다로 곱해준 결과인 λ
v 와 같다. (Av = λv)이것은 임의의 벡터를 λ 배 하는 행렬벡터곱으로 다시 쓸 수 있다.이러한 행렬의 열은 각 기저 벡터에 일어나는 변화를 나타내는데 단순히 λ배를 하므로 다음과 같아진다.영벡터를 만드는 벡터 v를 찾아야 하는데, 영이 아닌 것 중에서 찾아야 한다. (A - λI) v = 0행렬식이 0이 되는 것을 찾는다.
람다 λ 를 찾기 위해서는 기저벡터의 변환을 보여주는 행렬에서 대각선으로 람다를 뺀다.
이것의 행렬식이 0이 되는 값을 찾는다.
2차원 변환은 고유벡터가 무조건 존재하진 않는다.
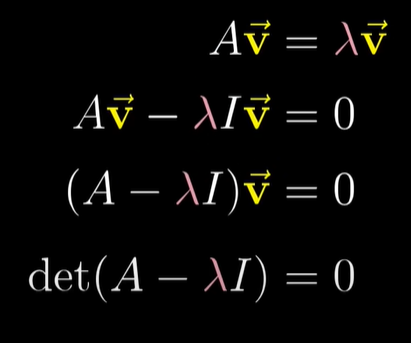

eigenbasis (고유기저)
대각행렬은 모든 기저벡터가 고유벡터이다.
대각선에 있는 값들이 고유값가 된다.
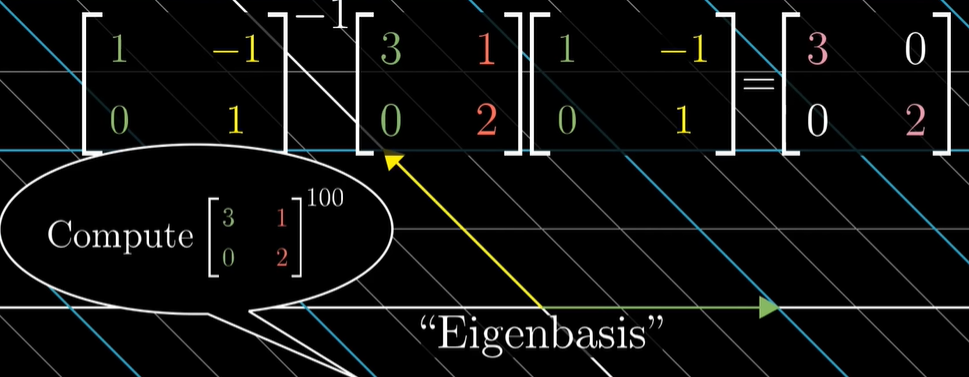
대각행렬이 다루기 좋은 이뉴는 스스로를 계속 곱해도 계산하기 쉽다는 것이다.
행렬을 100번 적용하면 기저 벡터들을 고유값의 100제곱으로 스케일링 하는 것과 동일하다.
선형변환이 고유벡터들을 많이 가지고 있다면 고유벡터가 기저벡터가 되도록 좌표계를 바꿀 수 있다.
위에서 배운 기저를 바꾸는 A^-1 M A 공식을 여기서 사용할 수 있다.
기저벡터이기도 한 고유벡터의 쌍, 즉 고유벡터를 기저로 사용할 때 '고유기저'(eigenbasis)라고 불린다.

Ch15. A quick trick for computing eigenvalues

1. 대각선 항목의 합은 고유치의 합과 같다.
더 잘 쓰이는 표현은 고유치의 평균이 두 대각선 항목의 평균과 같다는 것이다.
2. 행렬식(ad-bc)은 두 고유치의 곱과 같다.
고유치는 고유벡터를 얼마나 늘리는지를 나타낸다. 행렬식은 공간의 부피가 얼마나 확장하는지를 나타낸다.
3. 빠르게 고유치를 계산하는 식을 세울 수 있다. mean-product formula
위에서 다룬 합과 곱을 이용하여 곱을 합으로 표현할 수 있다. 거리를 산출하면 평균에서 양과 음으로 떨어진 고유치를 계산할 수 있다.


Pauli spin matrices
양자 역학 (quantum mechanics)에서 자주 등장하는 세 가지 행렬 세트를 살펴보자.
행렬의 고유치를 알면 그것이 설명하는 물리학과 깊은 관련이 있다.
세 가지 경우 모두 고유치의 평균은 0이다. 고유치의 곱도 모두 -1이다.
결국 고유치는 ±1 이다.

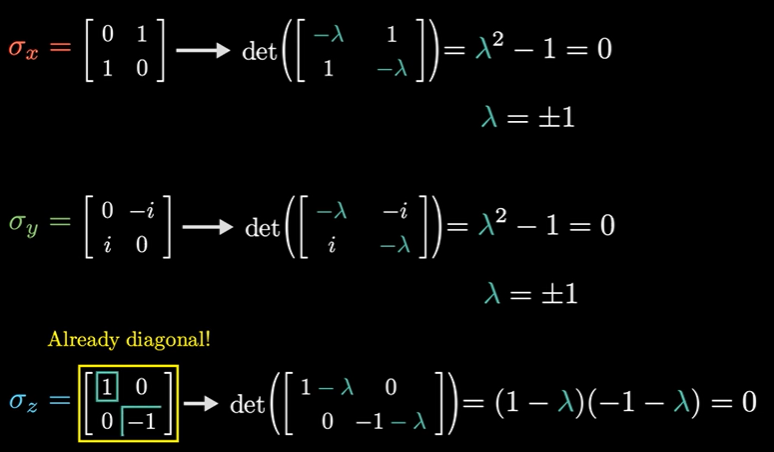
양자 역학의 맥락에서 이러한 행렬은 x, y, z 방향의 입자 스핀에 대해 수행할 수 있는 관찰을 설명한다.
고유치가 -1이라는 것은 관찰할 스핀 값이 그 사이에 연속적인 범위를 갖는 것이 아니라 완전히 한 방향이거나 완전히 다른 방향이라는 생각과 일치한다.
그런데, 사실 quick trick을 쓰지 않아도 정석적인 행렬식이 0이 되는 계산만으로도 고유치를 쉽게 구해낼 수 있다. 세 번째는 이미 대각행렬이므로 해당 대각선에 있는 항목이 고유치이다.
세 가지 행렬의 선형 조합을 취한 다음 고유치를 구하는 것. 좌표 [a, b, c]를 갖는 벡터의 일반적인 방향으로 스핀 관찰을 설명한다.


평균곱 공식을 찾는 것은 특성 항식의 근을 찾는 것과 근본적으로 다르지 않다.
전통적인 2차 방정식 근의 공식보다 더 가벼운 버전이라고 생각할 수 있지만, 진짜 장점은 기호가 적고, 각 기호가 더 많은 의미를 담고 있다는 것이다.
특성다항식을 만들지 않고도 행렬로부터 바로 고유치를 계산할 수 있는 것이 평균곱 공식의 큰 장점이다.
Ch16. Abstract vector spaces
선형대수를 공부하는 사람들은 보통 기저벡터를 바꾸는데 능숙할수록, 주어진 좌표계랑 상관없이 공간을 다룬다.
좌표계는 기저벡터를 어떻게 정하느냐에 따라 수시로 바뀐다.
행렬식이나 고유벡터같은 주제는 좌표계를 어떻게 정하는지랑 상관이 없다.
행렬식(determinant)는 변환이 면적을 얼마나 스케일링하는지를 나타내며,
고유벡터(eigenvector)는 변환이 일어나도 span을 벗어나지 않는 벡터이다.
함수는 그냥 다른 종류의 벡터일 뿐이다.
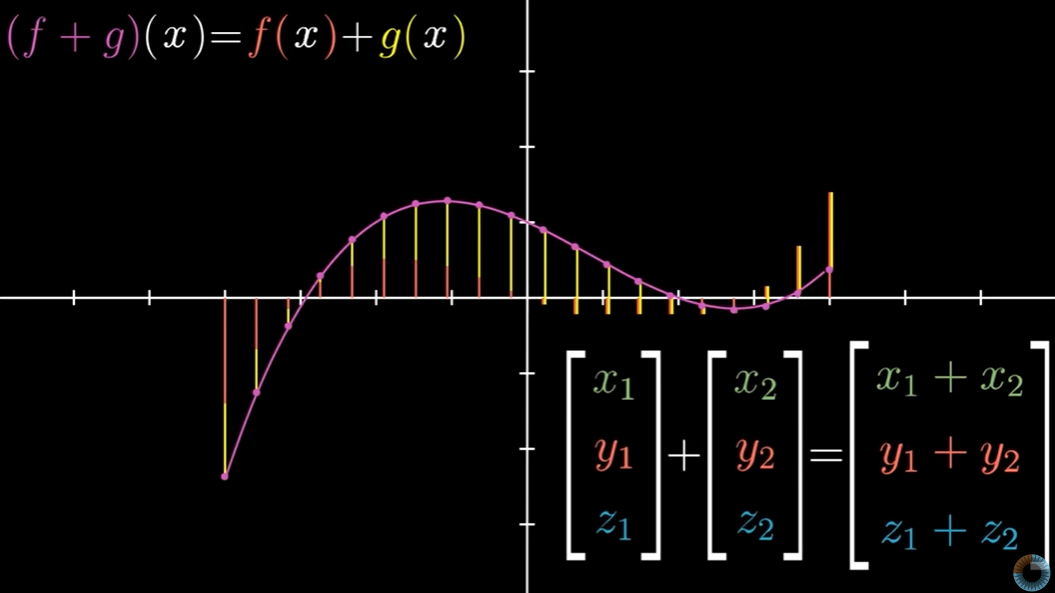
두 벡터를 더하는 것과 마찬가지로 두 함수를 더해 새로운 함수를 구하는 방법이 있다.
임의의 값 x에서 f+g의 함수값은 f(x) 와 g(x)의 합이다.
이것은 벡터에서 같은 좌표계끼리 더하는 것과 비슷하다.
함수에서는 무한히 많은 좌표계들을 더하는 셈이다.
함수값에 실수를 곱하는 것도 벡터에서 좌표계마다 실수배하는 것과 비슷하다.

함수의 미분은 함수를 변환시키는 데 연산이라고 부르는 것을 볼 수 있다.
함수의 변환이 '선형'이라는 것이 무슨 의미일까?
변환이 선형이라면 합과 실수배의 성질을 만족한다. 다른 말로, 선형변환이 합과 실수배를 보존한다.
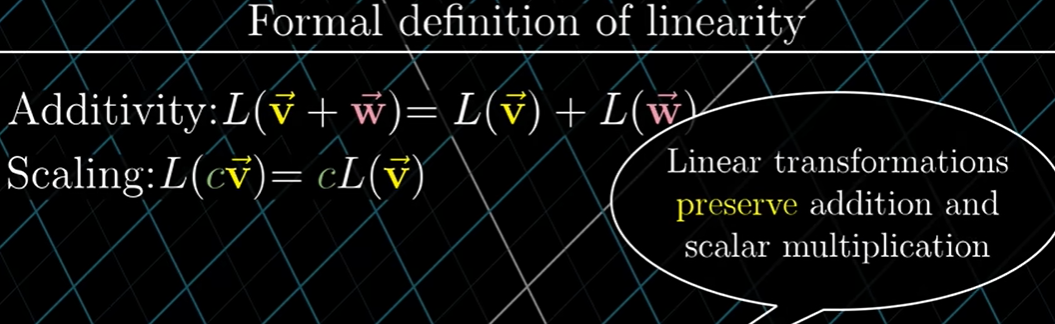
어떤 벡터든지 기저벡터의 실수배와 합으로 표현할 수 있기 때문에 벡터를 변환한 결과 역시 기저벡터를 변환한 것의 실수배와 합으로 표현할 수 있다.
이 방법은 함수에서도 성립한다. 미분에서 합과 실수배 성질을 자연스럽게 사용한다.
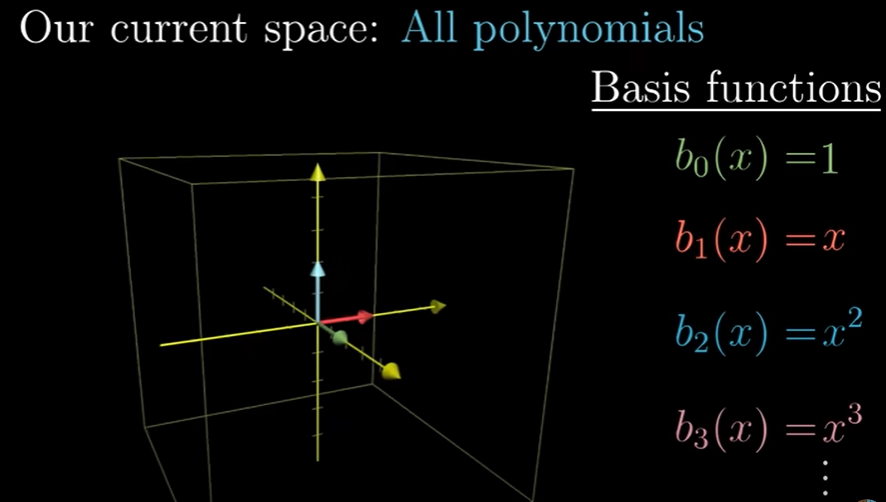
기저함수의 역할은 벡터에서 i-hat, j-hat, k-hat과 같다.
다항식이 임의의 최고차항을 가지기 때문에 기저함수는 무한히 많다.
다항식을 무한한 좌표를 가진 벡터로 생각하는 것뿐이다.
유한한 수의 좌표와 무한히 많은 0으로 이루어진다.

행렬 벡터곱과 미분한 것의 결과가 동일하게 표현됨을 확인할 수 있다.
4x를 미분한 것의 결과가 1*4로 4이다.
이것이 가능한 것은 미분(Derivative)이 선형(linear)이기 때문이다.
벡터를 공간에서의 화살표로 표현한 개념들이 함수에서도 사용되는 개념이다.

벡터란 무엇인가?
화살표의 집합이든, 숫자의 배열이든, 함수든, 어떻게 정의하든 선형대수학에서 개발한 선형변환, 영공간, 고유벡터, 내적 등의 개념을 사용할 수 있다.
화살표, 숫자배열, 함수 같은 것들을 벡터공간(vector spaces)이라고 한다.
벡터 합과 실수배에서 파생된 규칙을 정립해야 한다. '공리'(Axiom)라고 부른다.
여기에 적용이 되면 어떤 상황이든 사용자의 편의에 맞춰서 적용할 수 있다.
이것이 공식적이기 때문에 모든 책에서 선형변환을 '격자가 평행하고 균등하게 변하는 것'(Grid lines remain parallel and evenly spaced) 대신 합과 실수배로 정의하고 있는 이유이다.
현대에서는 벡터의 형태를 신경쓰지 않는다. 합과 실수배가 공리를 만족하게 정의되어 있으면 무엇이든 벡터가 될 수 있다.
예를 들어, 3이라는 숫자는 수학에서는 모든 '3배'들을 추상화한 개념이다. 한 가지 개념으로 모든 것들을 생각하게 해준다.

'Mathematics and Statistics' 카테고리의 다른 글
| Probability and Statistics_Khan [Unit 1~8] Probability (0) | 2024.01.19 |
|---|---|
| Review >> Essence of Linear Algebra_3Blue1Brown (1) | 2024.01.14 |
| Review >> Linear Algebra_Khan (2) | 2024.01.09 |
| Linear Algebra_Khan [3/3] 상호 좌표계(기저) (1) | 2024.01.09 |
| Linear Algebra_Khan [2/3] 행렬변환 (2) | 2024.01.03 |
